Is there a Mathematica equivalent to MATLAB's logspace?

Question

Possible Duplicate:
How can I get exactly 5 logarithmic divisions of an interval?

I want to use Table to generate a list of items, but want the indices to be logarithmically spaced. Is there a simple way of doing this, or will I have to explicitly run linearly spaced indices through Exp to get my list?

Answer 1

Here's a somewhat simpler way:

 logspace[a_, b_, n_] := 10.0^Range[a, b, (b - a)/(n - 1)]

This gives a sequence starting at 10^a and ending at 10^b, with n points logarithmically spaced, as does MATLAB's logspace() function.

Answer 2

I don't belive there is a build in function for this, however you can easily do it using Range

 fSpace[min_, max_, steps_, f_: Log] :=  
      InverseFunction[f] /@ Range[f@min, f@max, (f@max - f@min)/(steps - 1)]

Inverse functions are being used so it'll give warnings in cases where you should be cautius, however it works for Log and other invertible functions.

 fSpace[1, 1000, 4]

{1, 10, 100, 1000}

{fSpace[1, 1000, 30, Sqrt[#] &], fSpace[1, 1000, 30]} // ListPlot

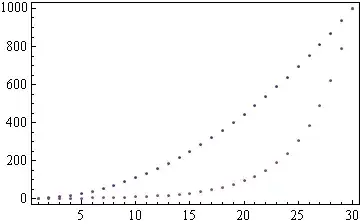
Update

I just discovered that you can in fact do even better out of the box by inverting the function only on the input range:

 fSpace[min_, max_, steps_, f_: Log] := 
  InverseFunction[ConditionalExpression[f[#], min < # < max] &] /@ 
  Range[f@min, f@max, (f@max - f@min)/(steps - 1)]

This still doesn't work arbitrarily, however it does help for instance selecting the positive square root in #^2&.