How to plot the GLSL expression

Question

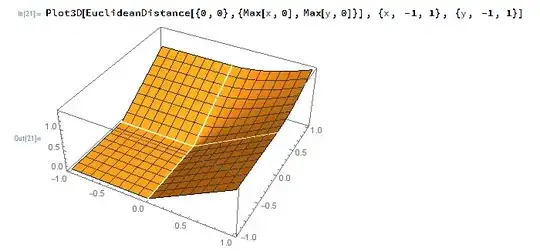
What's the most compact WL translation of this GLSL expression:

length(max(vec2(x,y),0))

?

My best attempt (using Wolfram Development Platform, not Mathematica) is

EuclideanDistance [{0,0},{Max[x,0],Max[y,0]}]

which works

but repeats Max.

This

EuclideanDistance [{0,0},Max[{x,y},0]]

fails thus:

score 3 · Accepted Answer · edited Jun 16 '20 at 09:23

3

Ramp

Norm @ Ramp @ {x,y}

Sqrt[Abs[Ramp[x]]^2 + Abs[Ramp[y]]^2]

Simplify[Ramp[x] - Max[x, 0]]

0

 Plot3D[Norm[Ramp@{x,y}],{x,-1,1},{y,-1,1}]

Norm[{x, y} UnitStep[{x, y}]]

Sqrt[Abs[x UnitStep[x]]^2 + Abs[y UnitStep[y]]^2]

Simplify[x UnitStep[x] - Max[x, 0]]

0

edited Jun 16 '20 at 09:23

Community

answered Jan 12 '18 at 02:00

kglr

Great. Thanks. Here's another Q: https://mathematica.stackexchange.com/questions/163598/translation-of-glsl-expression-2 – ChrisJJ Jan 13 '18 at 01:21

score 1 · Answer 2 · answered Jan 12 '18 at 01:43

1

I would just write it out

Sqrt[Max[0, x]^2 + Max[0, y]^2]

To me, this is clearer than the alternatives which include your version maybe these two

Sqrt[#.#] &[Max[0, #] & /@ {x, y}]
EuclideanDistance[{0, 0}, Max[0, #] & /@ {x, y}]

answered Jan 12 '18 at 01:43

halirutan