0

constants: 

S := 299792458;
Rem := 1;
Imm := 0;
c1 = 7.1966584528920068;
c2 = -2.8612955354362528*10^(-2);
c3 = 4.9904748273007211;
c4 = 1.1557482550800184;
c5 = 1.4462311508982122*10^4;
Of = 2.9899879533823599;
a0 = -4.0196213710349726*10^-1;
a1 = 9.9011244036818056;
a2 = 2.0237033052953829*10^-1;
a3 = 4.6135432671114094;
a4 = 3.3240796293189689*10^-1;
a5 = -2.6267966826701428*10^-1;

equations:

Ree[f_, wt_] = 
      c5/((1.0 + Exp[c1 - c2*f])*(1.0 + Exp[c3 - c4*wt])) + Of;

Ime[f_, wt_] = a0 + (a1/(1.0 + Exp[a2*(f + a3 + a4*wt + a5*f*wt)]));

El[f_, wt_] := Ree[f, wt] - I*Ime[f, wt];
Ma := Rem - I*Imm;

Z[wt_, f_, d_] := 
  Sqrt[Ma/El[f, wt]]*
   Tanh[I*2*Pi*f*10^9*d*(10^-3) *Sqrt[Ma*El[f, wt]]/S];
R[wt_, f_, d_] := (Z[wt, f, d] - 1)/(Z[wt, f, d] + 1);
RL[wt_, f_, d_] := 20*Log10[Abs[R[wt, f, d]]];

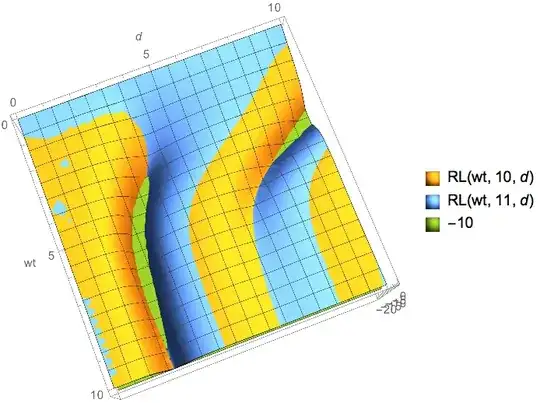
My attempt to find the roots using FindRoots function was not successful:

In[1024]:=  
 FindRoot[RL[wt, 10, d] == -10 && 
   RL[wt, 11, d] == -10, {{wt, 5, 0, 10}, {d, 5, 0, 10}}]

During evaluation of In[1024]:= FindRoot::lstol: The line search decreased the step size to within tolerance specified by AccuracyGoal and PrecisionGoal but was unable to find a sufficient decrease in the merit function. You may need more than MachinePrecision digits of working precision to meet these tolerances.

Out[1024]= {wt -> 2.99549, d -> 7.00699}

This point is far from the solution

In[1025]:= RL[2.9954853391692704`, 10, 7.006986346111831`]

Out[1025]= -3.4359

Please help me to solve this system of equations. "Solve" does not solve this system because of the inexact coefficients. "NSolve" return input.

Artyom Salnikov
  • 3
  • 3

1 Answers1

0

Use exact numbers

S = 299792458;
Rem = 1;
Imm = 0;
c1 = 7.1966584528920068 // Rationalize[#, 0] &;
c2 = -2.8612955354362528*10^(-2) // Rationalize[#, 0] &;
c3 = 4.9904748273007211 // Rationalize[#, 0] &;
c4 = 1.1557482550800184 // Rationalize[#, 0] &;
c5 = 1.4462311508982122*10^4 // Rationalize[#, 0] &;
Of = 2.9899879533823599 // Rationalize[#, 0] &;
a0 = -4.0196213710349726*10^-1 // Rationalize[#, 0] &;
a1 = 9.9011244036818056 // Rationalize[#, 0] &;
a2 = 2.0237033052953829*10^-1 // Rationalize[#, 0] &;
a3 = 4.6135432671114094 // Rationalize[#, 0] &;
a4 = 3.3240796293189689*10^-1 // Rationalize[#, 0] &;
a5 = -2.6267966826701428*10^-1 // Rationalize[#, 0] &;

Ree[f_, wt_] = c5/((1 + Exp[c1 - c2*f])*(1 + Exp[c3 - c4*wt])) + Of;

Ime[f_, wt_] = a0 + (a1/(1 + Exp[a2*(f + a3 + a4*wt + a5*f*wt)]));

El[f_, wt_] := Ree[f, wt] - I*Ime[f, wt];
Ma := Rem - I*Imm;

Z[wt_, f_, d_] := 
  Sqrt[Ma/El[f, wt]]*Tanh[I*2*Pi*f*10^9*d*(10^-3)*Sqrt[Ma*El[f, wt]]/S];
R[wt_, f_, d_] := (Z[wt, f, d] - 1)/(Z[wt, f, d] + 1);
RL[wt_, f_, d_] := 20*Log10[Abs[R[wt, f, d]]];

Plot (Plot3D) the functions to get good starting values

Plot3D[{RL[wt, 10, d], RL[wt, 11, d], -10}, {wt, 0, 10}, {d, 0, 10}, 
 AxesLabel -> Automatic, PlotLegends -> "Expressions"]

enter image description here

eqns = RL[wt, 10, d] == -10 && RL[wt, 11, d] == -10;

solns = FindRoot[eqns, {{wt, #[[1]], 0, 10}, {d, #[[2]], 0, 10}}] & /@
  {{3, 3}, {5, 8}, {9, 2}}

(* {{wt -> 3.06752, d -> 3.60292}, {wt -> 4.26555, d -> 8.12042}, 
    {wt -> 9.56317,d -> 2.05675}} *)

eqns /. solns

(* {True, True, True} *)

EDT: Alternatively, using a grid search

solnsSearch = 
 Union[Select[
    FindRoot[eqns, {{wt, #[[1]], 0, 10}, {d, #[[2]], 0, 10}}] & /@
     Tuples[Range[0, 10], 2], eqns /. # &], 
   SameTest -> (Norm[({wt, d} /. #1) - ({wt, d} /. #2)] < 10^-6 &)] // Quiet

(* {{wt -> 3.06752, d -> 3.60292}, {wt -> 4.26555, d -> 8.12042}, 
    {wt -> 9.56317, d -> 2.05675}} *)

The Select has already verified the solutions.

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198