How do I obtain an intersection of two or more list of lists conditioned on the first element of each sub-list?

Question

Given two lists like

list1 = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
list2 = {{2, 6}, {3, 9}, {4, 12}, {5, 15}};

I would like to produce an output like

listout = {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}

score 14 · Accepted Answer · edited Apr 13 '17 at 12:55

Good question. Second try.

Sow & Reap:

f1[a_List, b_List] := 
   Reap[Sow[#2, #] & @@@ a ~Join~ b, a[[All, 1]] ⋂ b[[All, 1]], List][[2, All, 1]]

Pick:

f2[a_List, b_List] :=
 With[{aa = a[[All, 1]], bb = b[[All, 1]]},
   {#[[1, 1]], #[[All, 2]]} & /@
      Pick[a ~Join~ b, aa ~Join~ bb, Alternatives @@ (aa ⋂ bb)] ~GatherBy~ First
 ]

Edit: Here is another method using GatherBy. While this method did not come to mind when I first wrote this answer I have used related methods for some time. It works by preconditioning GatherBy so that we collect the expressions we want at the beginning of the results and then discarding the rest. This is the same principle I used for How to Delete Elements from List1 appearing in List2? and more recently Complement on pre-sorted lists, and which jVincent used for Counting the population of integers.

f3[a_List, b_List] := 
  With[{pre = List /@ ( a[[All, 1]] ⋂ b[[All, 1]] )},
    {pre[[All, 1]], GatherBy[Join[pre, a, b], First][[;; Length@pre, 2 ;;, 2]]}\[Transpose]
  ]

At the expense of greater code length this can be made faster by using Szabolcs's inversion method with GatherBy:

f4[a_List, b_List] :=
 Module[{pre, first, all, n, a1, b1},
   {a1, b1} = {a[[All, 1]], b[[All, 1]]};
   n = Length[pre = a1 ⋂ b1];
   first = Join[pre, a1, b1];
   all = Join[a, b];
   {pre, Map[all[[#, 2]] &, 
      GatherBy[Range@Length@first, first[[#]] &][[;; n, 2 ;;]] - n]}\[Transpose]
 ]

Test:

list1 = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
list2 = {{2, 6}, {3, 9}, {4, 12}, {5, 15}, {5, 7}};

f1[list1, list2]

{{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}

I included {5, 7} in list2 to show that this is finding the intersection of the two lists and not merely repeats within a single list.

For those of us who cannot read infix: f2[a_, b_] := ({#1[[1, 1]], #1[[All, 2]]} & ) /@ GatherBy[ Cases[Join[a, b], {Alternatives @@ Intersection[a[[All, 1]], b[[All, 1]]], _}], First] — Mike Honeychurch, Dec 17 '12 at 06:56
Looks fine to me. Would be interested to know how Apply Alternative compares with the MemberQ test for larger lists. I normally use Alternative but forgot all about it when I wrote my answer — Mike Honeychurch, Dec 17 '12 at 06:57
@Mike Alternatives test quite a bit faster than MemberQ for me. For pure speed this seems best of what I've tried: Pick[#, First /@ #, Alternatives @@ inter] & @ Join[a, b] where inter is the first elements intersection. — Mr.Wizard, Dec 17 '12 at 07:10
Yes Pick will generally provide a much faster solution than e.g. Cases/Select if you can develop a Pick method. — Mike Honeychurch, Dec 17 '12 at 07:35

score 13 · Answer 2 · edited Dec 17 '12 at 07:55

13

this works for the given example:

ReplaceList[{list1, list2}, {{___, {a_, b_}, ___}, {___, {a_, c_}, ___}} :> {a, {b, c}}]

(* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}} *)

edited Dec 17 '12 at 07:55

Mr.Wizard

271,378
34
587
1,371

answered Dec 17 '12 at 07:38

kptnw

1,406
8
15

2

Very clever! However, this runs into problems if there are duplicates (in terms of first element) internally in either list. It is also rather slow on longer lists. Enthusiastic +1 nevertheless! – Mr.Wizard Dec 17 '12 at 07:46
2

An additional note: make sure you use RuleDelayed (:>) when working with named patterns on the right-hand side. This correctly localizes the symbols. I made this edit for you; I hope you don't mind. – Mr.Wizard Dec 17 '12 at 07:56
@Mr.Wizard Thanks for your vote, your editing, and many of your wonderful answers I learn and love :) – kptnw Dec 17 '12 at 10:51

kglr · Answer 3 · 2012-12-17T10:34:23.533

Update 3: A generalization for any number of lists and any column as the key:

 ClearAll[combineBy];
 combineBy[lists : __List, col_Integer] /; (col <= Min[Length /@ # & /@ {lists}]) := 
  With[{intNodes =  Alternatives @@ Intersection @@ (#[[col]] & /@ # & /@ {lists}),
  joined = GatherBy[Join[lists], #[[col]] &],
  othercols = DeleteCases[Range[Min[Length /@ # & /@ {lists}]], col]},
  {#[[1, col]], Join @@ #[[All, othercols]]} & /@
     Pick[joined, ! FreeQ[#[[1, col]], intNodes] & /@ joined]]

OP's example:

  list1 = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
  list2 = {{2, 6}, {3, 9}, {4, 12}, {5, 15}, {5, 7}};
  combineBy[list1, list2, 1]
  (* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}} *)
  combineBy[list1, list2, 2]
  (* {{9, {3, 3}}} *)

More examples:

  list3 = Table[RandomSample[Range[7], 3], {3}];
  list4 = Table[RandomSample[Range[7], 3], {4}];
  list5 = Table[RandomSample[Range[7], 3], {6}];

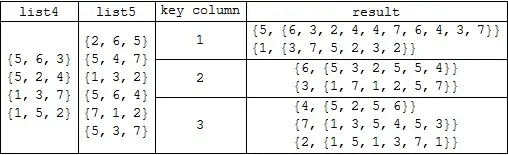
  Prepend[Prepend[{SpanFromAbove, SpanFromAbove,  #, 
   Column[combineBy[list4, list5, #]]} & /@ {2, 3},
   {Column@list4, Column@list5, 1, Column[combineBy[list4, list5, 1]]}],
   {"list4", "list5", "key column", "result"}] //
   Grid[#, Alignment -> {Center, Center}, Dividers -> All] &

enter image description here

  Prepend[Prepend[{SpanFromAbove, SpanFromAbove, #, 
   Column[combineBy[list3, list4, #]]} & /@ {2, 3},
   {Column@list3, Column@list4, 1, Column[combineBy[list3, list4, 1]]}],
   {"list3", "list4", "key column", "result"}] //
   Grid[#, Alignment -> {Center, Center}, Dividers -> All] &

enter image description here

  Prepend[Prepend[{SpanFromAbove, SpanFromAbove,  #, 
   Column[combineBy[list3, list5, #]]} & /@ {2, 3},
   {Column@list3, Column@list5, 1,  Column[combineBy[list3, list5, 1]]}],
   {"list3", "list5", "key column", "result"}] //
   Grid[#, Alignment -> {Center, Center}, Dividers -> All] &

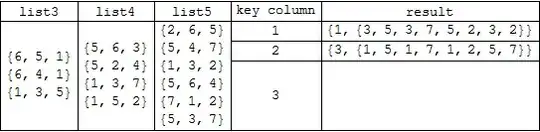
enter image description here

  Prepend[Prepend[{SpanFromAbove, SpanFromAbove, SpanFromAbove,  #, 
     Column[combineBy[list3, list4, list5, #]]} & /@ {2, 3},
    {Column@list3, Column@list4, Column@list5, 1,
      Column[combineBy[list3, list4, list5, 1]]}],
    {"list3", "list4", "list5", "key column", "result"}] //
   Grid[#, Alignment -> {Center, Center}, Dividers -> All] &

enter image description here

  ClearAll[combine];
  combine[list1_List, list2_List] := 
  With[{intNodes = Intersection[First /@ list1, First /@ list2], 
    joined =  GatherBy[Join[list1, list2], First]},
    {First[First@#],  Last[#]} & /@ (Transpose /@ 
    Select[joined, MemberQ[intNodes, #[[1, 1]]] &])]

 combine[list1, list2]
 (* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}} *)
 combine[list1, {{2, 6}, {3, 9}, {4, 12}, {5, 15}, {5, 7}}]
 (* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}} *)

(Updated with correction thanks to @Mr.W's comment: the second argument of Select is changed from Length[#]>2& in the original post to the correct version that accounts for the intersection of the first columns of the two lists.)

Update 2: Using Pick instead of Select:

ClearAll[combine2];
combine2[list1_List, list2_List] := 
 With[{intNodes = Intersection[First /@ list1, First /@ list2], 
   joined =  GatherBy[Join[list1, list2], First]}, 
 {#[[1, 1]], #[[-1]]} & /@ 
  (Transpose /@ Pick[joined, MemberQ[intNodes, #[[1, 1]]] & /@ joined])]

Funny, I was just trying Pick myself. See the comments below my answer. Great minds and all that. — Mr.Wizard, Dec 17 '12 at 07:12
@Mr.W, of the triplets (Cases, Select,Pick), Pick is almost always the first that I try ... and it rarely disappoints. — kglr, Dec 17 '12 at 07:38

score 7 · Answer 4 · answered Dec 17 '12 at 11:33

7

I like this one:

{#[[1,1]],#[[All,2]]}&/@Select[GatherBy[list1~Join~list2,First],Length[#]>1&]

(*{{2,{4,6}},{3,{9,9}},{4,{16,12}}}*)

answered Dec 17 '12 at 11:33

Murta

26,275
6
76
166

Mike Honeychurch · Answer 5 · 2012-12-17T08:06:42.397

Edit 1

processList[list1_, list2_] := Module[{intersection, tmp1, tmp2},

 (* find the intersection of the all the first elements *)
  intersection = Intersection[list1[[All, 1]], list2[[All, 1]]];

 (* now find cases in each list in which the first element is one of the intersecting   
  elements *)
  tmp1 = Cases[list1, {x_ /; MemberQ[intersection, x], __}];
  tmp2 = Cases[list2, {x_ /; MemberQ[intersection, x], __}];

  (* now gather all sub-lists based on the first element and map them to give the   
  desired output *)
  {#[[1, 1]], ##[[All, 2]]} & /@ GatherBy[Join[tmp1, tmp2], First]
  ]

test:

processList[list1, {{2, 6}, {3, 9}, {4, 12}, {5, 15}, {5, 7}}]
(* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}} *)

Edit 2

Since we're onto Pick methods :) ...this seems relatively concise. Two steps from above and then pick out the elements for output.

processList2[list1_, list2_] := Module[{intersection, tmp},

  intersection = Intersection[list1[[All, 1]], list2[[All, 1]]];
  tmp = {#[[1, 1]], ##[[All, 2]]} & /@ GatherBy[Join[list1, list2], First];
  Pick[tmp, tmp[[All, 1]] /. Thread[Rule[intersection, True]]]
  ]

list2 = {{2, 6}, {3, 9}, {4, 12}, {5, 15}, {5, 7}};
processList2[list1, list2]
(* {{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}  *)

For all of these Pick methods I'm not sure how efficient creating the stencil can be for this particular problem. If the stencil is efficiently created then Pick is a fast way of picking out elements from lists.

Re: Edit, that looks like a more intelligent approach than the one I just posted. I hope you don't mind if I borrow from it. :-) — Mr.Wizard, Dec 17 '12 at 06:21
@Mr.Wizard not sure how intelligent it is, or efficient. Just a stepwise approach. :) — Mike Honeychurch, Dec 17 '12 at 06:24
Please take a look at my answer now and tell me if you see anything wrong. — Mr.Wizard, Dec 17 '12 at 06:43
Perhaps I should insist on your removing infix notation before looking at it :) — Mike Honeychurch, Dec 17 '12 at 06:58

Nasser · Answer 6 · 2012-12-17T14:07:19.297

5

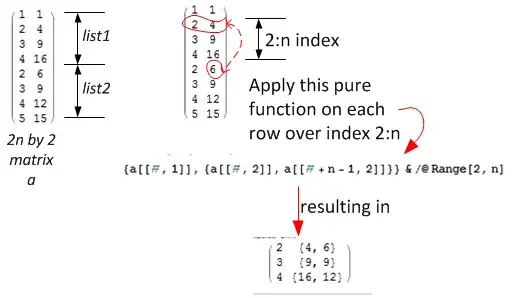
a = Join[list1, list2]
n = Length[list1];
{a[[#, 1]], {a[[#, 2]], a[[# + n - 1, 2]]}} & /@ Range[2, n]

![Mathematica graphics](https://i.stack.imgur.com/FXKvd.png)

Explanation: Use linear indexing. We have 2 matrices as input. list1 and list2. Each is an n by 2 size matrix. Joining them results in one 2n by 2 matrix called a. This diagram explains the algorithm enter image description here

edited Dec 17 '12 at 14:07

answered Dec 17 '12 at 07:12

Nasser

143,286
11
154
359

Am I correct in observing that this only works if the two lists have a common ordered subset, e.g. {2, 3, 4}? – Andrew Cheong Aug 25 '13 at 03:34

score 2 · Answer 7 · answered Dec 18 '12 at 12:16

2

Just for fun, a rule-based approach:

list2/.{{i_Integer/;!MemberQ[list1[[All,1]],i],x_}:>Sequence[],{i_Integer,x_}:>{i,{i/.(Rule@@@list1),x}}}

answered Dec 18 '12 at 12:16

Rolf Mertig

17,172
1
45
76

score 2 · Answer 8 · answered Nov 21 '23 at 10:09

Using Association - related functions (not yet available in 2012)

a = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
b = {{2, 6}, {3, 9}, {4, 12}, {5, 15}};
Cases[{, {, __}}] @
 KeyValueMap[List] @ Merge[# &] @ MapApply[Rule] @ Join[a, b]

{{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}

score 2 · Answer 9 · answered Nov 21 '23 at 10:47

GroupBy

WolframLanguageData["GroupBy",
  {"VersionIntroduced",  "DateIntroduced"}]

a = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
b = {{2, 6}, {3, 9}, {4, 12}, {5, 15}};
MapApply[List] @
Normal @ 
Select[Length @ # > 1 &] @ 
GroupBy[Join[a, b], First -> Last]

{{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}

Map[{#[[1, 1]], Flatten @ #[[All, 2 ;;]]} &] @
Values @ 
Select[Length@# > 1 &] @ 
GroupBy[Join[a, b], First]

{{2, {4, 6}}, {3, {9, 9}}, {4, {16, 12}}}

WolframLanguageData["WolframLanguageData", 
  {"VersionIntroduced",  "DateIntroduced"}]

score 0 · Answer 10 · answered Nov 21 '23 at 20:33

Cases[KeyValueMap[List]@GroupBy[Join[list1,list2],First->Last],{a_,{b_,c__}}->{a,{b,c}}]

(* {{2,{4,6}},{3,{9,9}},{4,{16,12}}} *)

list1x = {{1, 1}, {2, 4}, {3, 9}, {4, 16}};
list2x = {{2, 6}, {3, 9}, {4, 12}, {5, 15},{2,100},{2,2},{2,1}};

Cases[KeyValueMap[List]@GroupBy[Join[list1x,list2x],First->Last],{a_,{b_,c__}}->{a,{b,c}}]

(* {{2,{4,6,100,2,1}},{3,{9,9}},{4,{16,12}}} *)

How do I obtain an intersection of two or more list of lists conditioned on the first element of each sub-list?

10 Answers10

GroupBy

Linked

Related