Take data point from Circle

Question

I would like to draw a circle within triangle. In this case, I make it from 3 points.

then I followed program below:

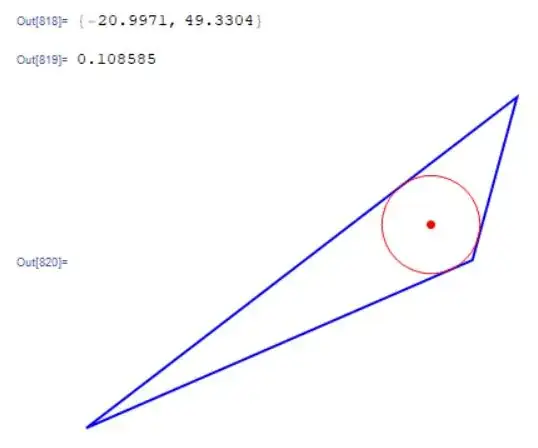
pA = {-21.7624, 48.8792}; pB = {-20.8074, 49.6132}; pC = {-20.9061, 49.2516};
lr = MeshRegion[{pA, pB, pC}, Triangle[Range@3]];
r1 = RegionDistance[InfiniteLine[{pA, pB}], {x, y}];
r2 = RegionDistance[InfiniteLine[{pB, pC}], {x, y}];
r3 = RegionDistance[InfiniteLine[{pC, pA}], {x, y}];
centerC = {x, y} /. NSolve[{r1 == r2, r2 == r3}, {x, y}, Reals];
centerC = Select[centerC, RegionMember[lr, #] &][[1]]
raioC = RegionDistance[Line[{pA, pB}], centerC]
Graphics[{EdgeForm[{Thick, Blue}], White, Triangle[{pA, pB, pC}], PointSize[Large], Red, Point@centerC, Red, Circle[centerC, raioC]}]

But I don't know how to take circle data points and the intersection point between a circle and triangle.

@C.E., I followed link https://mathematica.stackexchange.com/questions/57828/to-inscribe-a-circle-in-a-given-triangle — R.G., Jan 29 '18 at 16:03
It means to find the nearest points on the lines from the cirlce center and that's pretty standard formlulas. To be found in books on analytic geometry. — Andrew, Jan 29 '18 at 16:22
You can take a look at Marian MURESAN, Introduction to Mathematica with Applications, Springer, London, 2017, ISBN 978-3-319-52002-5. Marian — Marian Muresan, Jan 29 '18 at 15:56

score 6 · Answer 1 · answered Jan 29 '18 at 17:45

Use Insphere and RegionNearest:

pA={-21.7624,48.8792}; pB={-20.8074,49.6132}; pC={-20.9061,49.2516};

sphere = Insphere[{pA,pB,pC}]
center = First @ sphere;

pAB = RegionNearest[Line[{pA,pB}], center]
pBC = RegionNearest[Line[{pB,pC}], center]
pCA = RegionNearest[Line[{pC,pA}], center]

Sphere[{-20.9971, 49.3304}, 0.108585]

{-21.0633, 49.4165}

{-20.8924, 49.3018}

{-20.9538, 49.2308}

Visualization:

Graphics[{
    EdgeForm[Black], FaceForm[Green], Triangle[{pA,pB,pC}],
    sphere,
    PointSize[Large], Red, Point[{pAB,pBC,pCA}]
}]

Another possibility is to use RegionIntersection between the triangle and the circle, but that approach suffers from precision issues.

Take data point from Circle

1 Answers1