I would like to simulate birth process with time delay. Here is a reference ref on page 3. Note there is two species whereas in my case I have one species. So only equation (1) and (2) should be considered. My code does not give desired result. Any suggestion.
Here is the code for Birth Death Process without delay(propensity rate depends on current population).
$\emptyset\xrightarrow[]{\text{$\lambda$ X}} X\quad \quad$ birth
$X\xrightarrow[]{\text{$\mu$ X}} \emptyset \quad \quad$ death
SeedRandom@2;
With[{λ = 4, μ = 1, initialPop = 10}, sim = NestList[(
a1 = λ #[[2]];
a2 = μ #[[2]];
a0 = Total@{a1, a2};
reaction = 1/a0 Accumulate@{a1, a2};
pos = First@FirstPosition[reaction, _?(RandomReal[] < # &)];
Δt =
RandomVariate@ExponentialDistribution[a1 + a2];
Which[
pos == 1, {#[[1]] + Δt, #[[2]] + 1},
pos == 2, {#[[1]] + Δt, #[[2]] - 1}
]
) &, {0, initialPop}, 20]];
sim;
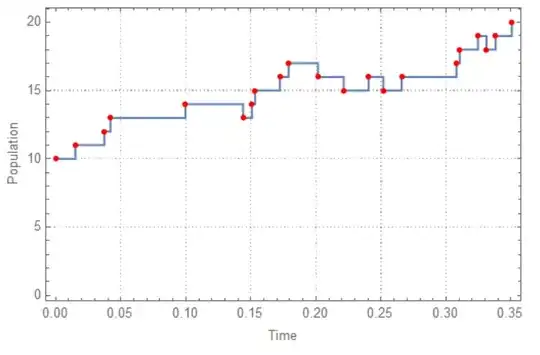
ListLinePlot[sim, Epilog -> {Red, PointSize[Medium], Point[sim]},
Frame -> True, PlotTheme -> "Detailed",
FrameLabel -> {"Time", "Population"}, ImageSize -> Large,
InterpolationOrder -> 0]
Now Assume there is delay on birth reaction.
$\emptyset\xrightarrow[]{\text{$\lambda$ X}} X\quad \quad$ birth has a delay
$X\xrightarrow[]{\text{$\mu$ X}} \emptyset \quad \quad$ death has no delay
- Sample reaction time $t_1\sim Exp(\lambda X+\mu X)$
- Choose a reaction.
- If it is a death set $X=X-1$ and new time is $t_1$.
- If it is a birth sample $t_d\sim Gamma(4,2)$
- Put $t_1+t_d$ into queue.
- Sample new reaction time $t_w\sim Exp(\lambda X+\mu X)$
- If $t_1+t_d<t_1+t_w$ set $X=X+1$. New time $t_1+t_d$
- If $t_1+t_d>=t_1+t_w$
- Choose a reaction.
- If it is a death set $X=X-1$.
- If it is a birth set $X=X$. No birth. New time $t_1+t_w$
Repeat
SeedRandom@2; With[{λ = 30, μ = 1, initialPop = 10}, sim = NestList[( a1 = λ #[[2]]; a2 = μ #[[2]]; a0 = Total@{a1, a2}; reaction = 1/a0 Accumulate@{a1, a2}; pos = First@FirstPosition[reaction, _?(RandomReal[] < # &)]; pos2 = First@FirstPosition[reaction, _?(RandomReal[] < # &)]; t = RandomVariate@ExponentialDistribution[a1 + a2]; td = RandomVariate@GammaDistribution[4, 2]; tw = RandomVariate@ExponentialDistribution[a1 + a2]; Which[ pos == 2, {#[[1]] + t, #[[2]] - 1}, pos == 1, Which[ t + td < t + tw, {#[[1]] + t + td, #[[2]] + 1}, t + td >= t + tw, Which[ pos2 == 2, {#[[1]] +t + tw, #[[2]] - 1}, pos2 == 1, {#[[1]] + t + tw, #[[2]]} ] ] ] ) &, {0, initialPop}, 100]]; sim; ListLinePlot[sim, Epilog -> {Red, PointSize[Medium], Point[sim]}, Frame -> True, PlotTheme -> "Detailed", FrameLabel -> {"Time", "Population"}, ImageSize -> Large, InterpolationOrder -> 0]
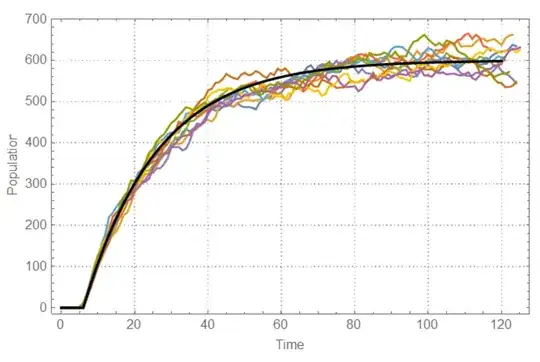
EDIT: Let's look at Pure Birth process(there is no death).
Here is the code without delay.
SeedRandom@2
With[{A = 5, initialPop = 10}, sim = NestList[(
Δt =
RandomVariate@ExponentialDistribution[A #[[2]]];
{#[[1]] + Δt, #[[2]] + 1}
) &, {0, initialPop}, 10]];
ListLinePlot[sim, Epilog -> {Red, PointSize[Medium], Point[sim]},
Frame -> True, PlotTheme -> "Detailed",
FrameLabel -> {"Time", "Population"}, ImageSize -> Large,
InterpolationOrder -> 0]
Here is the algorithm for delayed Pure Birth process
- Sample reaction time $t_1\sim Exp(\lambda X)$
- Sample delay time $t_{d_1}\sim Gamma(4,2)$
- Put $s_1=t_1+t_{d_1}$ into stack. Stack={$s_1$}
- Sample new reaction time $t_2\sim Exp(\lambda X)$
- If $t_1+t_2<s_1$, sample new delay time $t_{d_2}\sim Gamma(4,2)$ and Put $s_2=t_1+t_2+t_{d_2}$ into stack. Stack={$s_1$,$s_2$}. Order stack min to max. Min will be birth time if there is a birth in the future.
- If $t_1+t_2>=s_1$, let X=X+1. Remove $s_1$ from stack. set time $s_1$
- Repeat
I don't know how to code this. Any suggestion.





[[3]]'s in your definition ofa1anda2should be[[2]]'s. – Chris K Feb 03 '18 at 03:00