Plotting direction field of a system

Question

I have the next system:

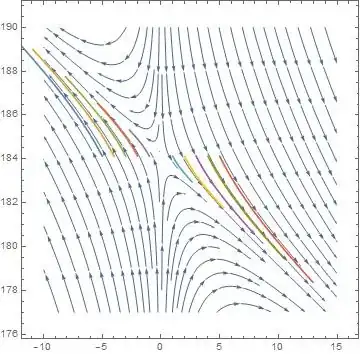
I have plot the direction field of the system.

The equations are:

eqH = HH'[t] == (bH/NN)*(NN - CC[t] - HH[t])*HH[t] - (sH*aH)*HH[t]
eqC = CC'[t] == (bC/NN)*(NN - CC[t] - HH[t])*CC[t] - (sC + aC)*CC[t]
eqS = SS[t] == NN - HH[t] - CC[t]

And values for parameters:

NN := 400
sS := 1/5
sC := 1/7
sH := 1/5
bC := 0.45
bH := 0.4
aC := 0.1
aH := 0.1

Here is what I tried:

sp = StreamPlot[{eqH, eqC}, {HH[t], -220, 200}, {CC[t], -200, 200}];
soln[x0_?NumericQ] := 
   First@NDSolve[{eqH, HH[0] == 0, eqC, CC[0] == 184.127}, {x, y}, {t, 
   200, 200}];
 Show[sp, ParametricPlot[
       Evaluate[{HH[t], CC[t]} /. soln[#] & /@ Range[-200, 200, 1]], {t, 
       200, 200}, PlotRange -> All, MaxRecursion -> 8, 
       AxesLabel -> {"x", "y"}, PlotStyle -> Red]]

But it's wrong, I really don't know how to plot the direction...

You have many syntactic errors (missing semicolons, variables labelled by upper-case-first names, confusion between = and :=, an iteration variable the non-sensical CC[t], and more. — David G. Stork, Feb 07 '18 at 00:45

score 3 · Accepted Answer · answered Feb 07 '18 at 04:35

Are you looking for something like this?

NN = 400; sS = 1/5; sC = 1/7; sH = 1/5; bC = 0.45; bH = 0.4; aC = 0.1; aH = 0.1;

sp = StreamPlot[{(bH/NN)*(NN - CC[t] - HH[t])*HH[t] - (sH*aH)*
      HH[t], (bC/NN)*(NN - CC[t] - HH[t])*CC[t] - (sC + aC)*
      CC[t]}, {HH[t], -10, 15}, {CC[t], 177, 190}];

soln[x0_?NumericQ] := First@NDSolve[{eqH, HH[0] == x0, eqC, CC[0] == 184.127}, {HH, 
     CC}, {t, 0, 5}];

pp1 = ParametricPlot[Evaluate[{HH[t], CC[t]} /. soln[#] & /@ Range[-5, 5, 1]], {t, 0, 
    5}, Frame -> True];

Show[{sp, pp1}]

Plotting direction field of a system

1 Answers1