Mathematica Plot Recursion Accuracy

Question

Mathematica has the neat feature to sample the domain of a plot function adaptively, using recursion on a mesh in the function's domain. The set of initial points is controlled by PlotPoints, the maximum number of recursions by MaxRecursion. The automatic recursion stops when some pre-defined accuracy limit is reached. Now I want the recursion to become more accurate than it is with the standard settings. For this, neither a larger number of PlotPoints is appropriate, because is increases the mesh density everywhere, nor a larger number of MaxRecursion, because the recursion automatically stops as the algorithm thinks the result is accurate enough. Which option do I need to change in order to increase the desired accuracy of the recursion?

Answer 1

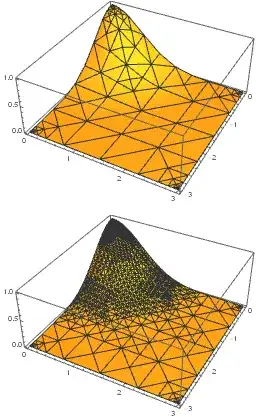
Thanks to one comment, I found a satisfactory solution: The recursion accuracy can be adjusted using Method -> {Refinement -> {ControlValue -> 0.05}}, where smaller values lead to a better accuracy and a finer mesh.

An example of 3D plots with lower and higher accuracy:

Plot3D[Exp[-x^2 - y^2], {x, 0, 3}, {y, -3, 0}, PlotRange -> Full,
  Mesh -> All, PlotPoints -> 5, MaxRecursion -> 5]
Plot3D[Exp[-x^2 - y^2], {x, 0, 3}, {y, -3, 0}, PlotRange -> Full, 
  Mesh -> All, PlotPoints -> 5, MaxRecursion -> 5, 
  Method -> {Refinement -> {ControlValue -> 0.05}}]