Solving Navier-Stokes equations for a steady-state compressible viscous flow in a 2D axisymmetric step

Question

Note: you may apply or follow the edits on the code here in this GitHub Gist

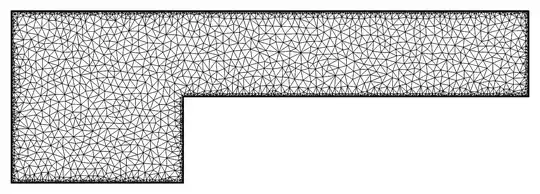
I'm trying to follow this post to solve Navier-Stokes equations for a compressible viscous flow in a 2D axisymmetric step. The geometry is :

lc = 0.03;
rc = 0.01;
xp = 0.01;
c = 0.005;
rp = rc - c;
lp = lc - xp;
Subscript[T, 0] = 300;
Subscript[\[Eta], 0] = 1.846*10^-5;
Subscript[P, 1] = 6*10^5 ;
Subscript[P, 0] = 10^5;
Subscript[c, P] = 1004.9;
Subscript[c, \[Nu]] = 717.8;
Subscript[R, 0] = Subscript[c, P] - Subscript[c, \[Nu]];
\[CapitalOmega] = RegionDifference[
   Rectangle[{0, 0}, {lc, rc}], 
   Rectangle[{xp, 0}, {xp + lp, rp}]];

And meshing:

Needs["NDSolve`FEM`"];
mesh = ToElementMesh[\[CapitalOmega], 
   "MaxBoundaryCellMeasure" -> 0.00001, 
   MaxCellMeasure -> {"Length" -> 0.0008}, 
   "MeshElementConstraint" -> 20, MeshQualityGoal -> "Maximal"][
  "Wireframe"]

Where the model is axisymmetric around the x axis, the governing equations including conservation equations of mass, momentum and heat can be written as:

$$ \frac{\partial}{\partial x}\left( \rho \nu_x \right)+\frac{1}{r}\frac{\partial }{\partial r}\left(r \rho \nu_r\right)=0 \tag{1}$$

$$\frac{\partial}{\partial x}\left( \rho \nu_x^2+\mathring{R} \rho T \right)+\frac{1}{r}\frac{\partial}{\partial r}\left( r \left( \rho \nu_r \nu_x + \eta \frac{\partial \nu_x}{\partial r} \right)\right) \tag{2}$$

$$ \frac{\partial}{\partial x}\left( \rho \nu_x \nu_r+\eta \frac{\partial \nu_r}{\partial x} \right)+ \frac{1}{r}\frac{\partial}{\partial r}\left( r \left( \rho \nu_r ^2 +\mathring{R} \rho T \right) \right)=0 \tag{3}$$

$$\rho c_\nu\left( \nu_x \frac{\partial T}{\partial x} + \nu_r \frac{\partial T}{\partial r} \right)+ \mathring{R} \rho T \left( \frac{1}{r}\frac{\partial}{\partial r} \left( r \nu_r \right)+ \frac{\partial \nu_x}{\partial x} \right)+ \eta \left( 2 \left( \frac{\partial \nu_x}{\partial x} \right)^2+ 2 \left( \frac{\partial \nu_r}{\partial r} \right)^2+ \left( \frac{\partial \nu_r}{\partial x}+ \frac{\partial \nu_x}{\partial r} \right)^2 \\ -\frac{2}{3}\left( \frac{1}{r} \frac{\partial}{\partial r}\left( r \nu_r \right) + \frac{\partial \nu_x}{\partial x} \right)^2 \right)=0 \tag{4}$$

eqn1 = D[\[Rho][x, r]*Subscript[\[Nu], x][x, r], x] + 
    D[r*\[Rho][x, r]*Subscript[\[Nu], r][x, r], r]/r == 0 ;
eqn2 = D[\[Rho][x, r]*Subscript[\[Nu], x][x, r]^2 + 
      Subscript[R, 0] \[Rho][x, r]*T[x, r], x] + 
    D[r*(\[Rho][x, r]*Subscript[\[Nu], x][x, r]*
          Subscript[\[Nu], r][x, r] + 
         Subscript[\[Eta], 0]*D[Subscript[\[Nu], x][x, r], r]), r]/
     r == 0 ;
eqn3 = D[\[Rho][x, r]*Subscript[\[Nu], x][x, r]*
       Subscript[\[Nu], r][x, r] + 
      Subscript[\[Eta], 0]*D[Subscript[\[Nu], r][x, r], x], x] + 
    D[r*(\[Rho][x, r]*Subscript[\[Nu], r][x, r]^2 + 
         Subscript[R, 0] \[Rho][x, r]*T[x, r]), r]/r == 0;
eqn4 = Subscript[
     c, \[Nu]]*\[Rho][x, 
      r]*(Subscript[\[Nu], x][x, r]*D[T[x, r], x] + 
       Subscript[\[Nu], r][x, r]*D[T[x, r], r]) + 
    Subscript[R, 0]*\[Rho][x, r]*
     T[x, r]*(D[Subscript[\[Nu], x][x, r], x] + 
       D[r*Subscript[\[Nu], r][x, r], x]/r) + (2*
        D[Subscript[\[Nu], x][x, r], x]^2 + 
       2*D[Subscript[\[Nu], r][x, r], 
          r]^2 + (D[Subscript[\[Nu], x][x, r], r] + 

          D[Subscript[\[Nu], r][x, r], 
           x])^2 - ((D[Subscript[\[Nu], x][x, r], x] + 
            D[r*Subscript[\[Nu], r][x, r], x]/r)^2)*2/3)*
     Subscript[\[Eta], 0] == 0;
eqns = {eqn1, eqn2, eqn3, eqn4};

And the boundary conditions are:

1. constant pressure at inlet
2. constant pressure at outlet
3. axis of symmetry
4. no slip

Implemented as

bc1 = Subscript[R, 0] \[Rho][0, r]*Subscript[T, 0] == Subscript[P, 1] 
bc2 = Subscript[R, 0] \[Rho][lc, r]*Subscript[T, 0] == Subscript[P, 0]
bc3 = DirichletCondition[{Subscript[\[Nu], r][x, 0] == 0, 
   D[Subscript[\[Nu], r][x, r], r] == 0, 
   D[Subscript[\[Nu], x][x, r], r] == 0, D[\[Rho][x, r], r] == 0, 
   D[T[x, r], r] == 0}, r == 0 && (0 <= x <= xp  )] 
bc4 = DirichletCondition[{Subscript[\[Nu], r][x, r] == 0, 
    Subscript[\[Nu], x][x, r] == 
     0}, (0 <= r <= rp && x == xp ) || (r == rp && 
      xp <= x <= xp + lp)  || (r == rc && 0 <= x <= lc) ] == 0
bcs = {bc1, bc2, bc3, bc4};

When I try to solve the equations:

{\[Nu]xsol, \[Nu]rsol, \[Rho]sol, Tsol} = 
  NDSolveValue[{eqns, , bcs}, {Subscript[\[Nu], x], Subscript[\[Nu], 
    r], \[Rho], T}, {x, r} \[Element] mesh, 
   Method -> {"FiniteElement", 
     "InterpolationOrder" -> {Subscript[\[Nu], x] -> 2, 
       Subscript[\[Nu], r] -> 2, \[Rho] -> 1, T -> 1}, 
     "IntegrationOrder" -> 5}];

I get the errors:

NDSolveValue::femnr: {x,r}[Element] is not a valid region specification.

and

Set::shape: Lists {[Nu]xsol,[Nu]rsol,Tsol,[Rho]sol} and NDSolveValue[<<1>>] are not the same shape.

Googling the errors does not offer that much of help (e.g. here). I would appreciate if you could help me know What is the issue and how I can solve it.

P.S.1. The NDSolveValue femnr error was caused by [ "Wireframe"] term at the end of meshing command changing it to

mesh = ToElementMesh[\[CapitalOmega], 
   "MaxBoundaryCellMeasure" -> 0.00001, 
   MaxCellMeasure -> {"Length" -> 0.0008}, 
   "MeshElementConstraint" -> 20, MeshQualityGoal -> "Maximal"];
mesh["Wireframe"]

resolves the issue.

P.S.2. There is an extra ==0 at the end of boundary condition 4 it was edited to:

bc4 = DirichletCondition[{Subscript[\[Nu], r][x, r] == 0, 
    Subscript[\[Nu], x][x, r] == 
     0}, (0 <= r <= rp && x == xp) || (r == rp && 
      xp <= x <= xp + lp) || (r == rc && 0 <= x <= lc)];

at this moment the second error still persists and a new error was added:

NDSolveValue::deqn Equation or list of equations expected instead of Null in the first argument ...

P.S.3 There were multiple issues. So I decided to use this Github Gist to further edit the code.

Answer 1

I prepared a solver for the steady axisymmetric flow of a viscous incompressible fluid for Reynolds numbers up to 1000 (but it is possible more, up to loss of stability) in geometry, which the author discusses. After discussing my decision, we will move on to the compressible flow, but I do not promise that it will be fast. For the solution, I used a standard task, which was published in the documentation since version 11. I even saved the notation for the solution to be recognizable. To solve a nonlinear problem, I used the fixed-point method. Here is an example of solving a problem with a Reynolds number of 1000. If you want to increase this number, you must decrease the parameter MaxCellMeasure.

lc = 3;
rc = 1;
xp = 1;
c = .5;
rp = rc - c;
lp = lc - xp;
K = 25; Re0 = 1000; h = .001;
u0[y_] := (rc^2 - y^2)/2;

\[CapitalOmega] = 
  RegionDifference[Rectangle[{0, h}, {lc, rc}], 
   Rectangle[{xp, rp}, {lc, rc}]];
UX[0][x_, y_] := 0;
VY[0][x_, y_] := 0;
Do[
  {UX[i], VY[i]} = 
   NDSolveValue[{{Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             u[x, y], {x, y}]), {x, y}] - D[u[x, y], y]*y/(y^2 + 0.) + 
\!\(\*SuperscriptBox[\(p\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[u[x, y], x] +
          Re0*VY[i - 1][x, y]*D[u[x, y], y], 
        Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             v[x, y], {x, y}]), {x, y}] + v[x, y]/(y^2 + 0.) - 
         D[v[x, y], y]*y/(y^2 + 0.) + 
\!\(\*SuperscriptBox[\(p\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[v[x, y], x] +
          Re0*VY[i - 1][x, y]*D[v[x, y], y], 
        D[y*u[x, y], x] + D[y*v[x, y], y]} == {0, 0, 0} /. \[Mu] -> 
       1, {
      DirichletCondition[u[x, y] == u0[y], x == 0.], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       0 <= x <= lc && y == rc || y == rp], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       x == xp && rp <= y <= rc],
      DirichletCondition[p[x, y] == 0, x == lc], 
      DirichletCondition[v[x, y] == 0, y == h]}}, {u, 
     v}, {x, y} \[Element] \[CapitalOmega], 
    Method -> {"FiniteElement", 
      "InterpolationOrder" -> {u -> 2, v -> 2, p -> 1}, 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.0005}}], {i, 1, K}];
StreamDensityPlot[{UX[K][x, y], 
  VY[K][x, y]}, {x, y} \[Element] \[CapitalOmega], 
 StreamPoints -> Fine, StreamStyle -> LightGray, 
 PlotLegends -> Automatic, VectorPoints -> Fine, 
 ColorFunction -> "TemperatureMap", FrameLabel -> {"x", "y"}]

{ContourPlot[UX[K][x, y], {x, y} \[Element] \[CapitalOmega], 
  PlotLegends -> Automatic, Contours -> 20, PlotPoints -> 25, 
  ColorFunction -> "TemperatureMap", AxesLabel -> {"x", "y"}, 
  PlotLabel -> u], 
 ContourPlot[VY[K][x, y], {x, y} \[Element] \[CapitalOmega], 
  PlotLegends -> Automatic, Contours -> 20, PlotRange -> All, 
  PlotPoints -> 50, ColorFunction -> "TemperatureMap", 
  AxesLabel -> {"x", "y"}, PlotLabel -> v], 
 ContourPlot[
  Norm[{UX[K][x, y], VY[K][x, y]}], {x, y} \[Element] \[CapitalOmega],
   PlotLegends -> Automatic, Contours -> 20, PlotRange -> All, 
  PlotPoints -> 50, ColorFunction -> "TemperatureMap", 
  AxesLabel -> {"x", "y"}, PlotLabel -> Sqrt[u^2 + v^2]]}

How can we know that the solution converges? Let us consider a simple estimate for the difference of two solutions at neighboring steps:

ListLogPlot[
 Table[Sum[Abs[UX[i][x, xp/2] - UX[i - 1][x, xp/2]], {x, 0, lc, .01}]/
   Sum[1, {x, 0, lc, .01}], {i, 1, K}], Filling -> Axis]

In this example, we see a rapid convergence with increasing K.

It was possible to make a solver for the isentropic flow. Here is an example of a flow with subsonic and supersonic speed in an axisymmetric channel with the geometry proposed by the author. The Reynolds number is 500. The Mach number at the exit from the channel is 2.5. A solver for an incompressible fluid is used with the necessary corrections that take into account the compressibility.

lc = 3;
rc = 1;
xp = 1;
c = .5;
rp = rc - c;
lp = lc - xp;  q = .4;
K = 25; Re0 = 500; h = .001; M = 1.; Re1 = Re0/M^2;
u0[y_] := (rc^2 - y^2)/2;
    \[CapitalOmega] = 
  RegionDifference[Rectangle[{0, h}, {lc, rc}], 
   Rectangle[{xp, rp}, {lc, rc}]];
UX[0][x_, y_] := 0;
VY[0][x_, y_] := 0;
\[CapitalRho][0][x_, y_] := 1;
Do[
  {UX[i], VY[i], \[CapitalRho][i]} = 
   NDSolveValue[{{Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             u[x, y], {x, y}]), {x, y}] - D[u[x, y], y]*y/(y^2 + 0.) +
          Re1*(Abs[\[CapitalRho][i - 1][x, y]]^q)*
\!\(\*SuperscriptBox[\(\[Rho]\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[u[x, y], x] +
          Re0*VY[i - 1][x, y]*D[u[x, y], y], 
        Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             v[x, y], {x, y}]), {x, y}] + v[x, y]/(y^2 + 0.) - 
         D[v[x, y], y]*y/(y^2 + 0.) + 
         Re1*(Abs[\[CapitalRho][i - 1][x, y]^q])*
\!\(\*SuperscriptBox[\(\[Rho]\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[v[x, y], x] +
          Re0*VY[i - 1][x, y]*D[v[x, y], y], 
        D[y*\[CapitalRho][i - 1][x, y]*u[x, y], x] + 
         D[y*\[CapitalRho][i - 1][x, y]*v[x, y], y]} == {0, 0, 
        0} /. \[Mu] -> 1, {
      DirichletCondition[{u[x, y] == u0[y]}, x == 0.], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       0 <= x <= lc && y == rc || y == rp], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       x == xp && rp <= y <= rc],
      DirichletCondition[\[Rho][x, y] == 1, x == lc], 
      DirichletCondition[v[x, y] == 0, y == h]}}, {u, 
     v, \[Rho]}, {x, y} \[Element] \[CapitalOmega], 
    Method -> {"FiniteElement", 
      "InterpolationOrder" -> {u -> 2, v -> 2, \[Rho] -> 1}, 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.0005}}], {i, 1, K}];
{ContourPlot[\[CapitalRho][K][x, 
   y], {x, y} \[Element] \[CapitalOmega], PlotLegends -> Automatic, 
  Contours -> 20, PlotPoints -> 25, ColorFunction -> "TemperatureMap",
   AxesLabel -> {"x", "y"}, PlotLabel -> \[Rho]], 
 ContourPlot[
  Norm[{UX[K][x, y], VY[K][x, y]}]/\[CapitalRho][K][x, y]^(q/2), {x, 
    y} \[Element] \[CapitalOmega], PlotLegends -> Automatic, 
  Contours -> 20, PlotRange -> All, PlotPoints -> 50, 
  ColorFunction -> "TemperatureMap", AxesLabel -> {"x", "y"}, 
  PlotLabel -> "M"]}

Distribution of density and Mach number

Let's add another pair of Fig. for the velocity field and the convergence of the method in the case of a compressible flow.

StreamDensityPlot[{UX[K][x, y], 
  VY[K][x, y]}, {x, y} \[Element] \[CapitalOmega], 
 StreamPoints -> Fine, StreamStyle -> LightGray, 
 PlotLegends -> Automatic, VectorPoints -> Fine, 
 ColorFunction -> "TemperatureMap", FrameLabel -> {"x", "y"}]

ListLogPlot[
 Table[Sum[Abs[UX[i][x, xp/2] - UX[i - 1][x, xp/2]], {x, 0, lc, .01}]/
   Sum[1, {x, 0, lc, .01}], {i, 1, K}], Filling -> Axis]

In the case of a compressible viscous flow with a given pressure at the inlet and outlet, I recommend the following code

lc = 3;
rc = 1;
xp = 1;
c = .5;
rp = rc - c;
lp = lc - xp; q = .4;
K = 17; Re0 = 100; h = .001; M0 = 1; Re1 = Re0/M0^2;
u0[y_] := (rc^2 - y^2)/2;
\[CapitalOmega] = 
  RegionDifference[Rectangle[{0, h}, {lc, rc}], 
   Rectangle[{xp, rp}, {lc, rc}]];
UX[0][x_, y_] := 0;
VY[0][x_, y_] := 0;
\[CapitalRho][0][x_, y_] := 1;
Do[
  {UX[i], VY[i], \[CapitalRho][i]} = 
   NDSolveValue[{{Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             u[x, y], {x, y}]), {x, y}] - D[u[x, y], y]/y + 
         Re1*(Abs[\[CapitalRho][i - 1][x, y]]^q)*
\!\(\*SuperscriptBox[\(\[Rho]\), 
TagBox[
RowBox[{"(", 
RowBox[{"1", ",", "0"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[u[x, y], x] +
          Re0*VY[i - 1][x, y]*D[u[x, y], y], 
        Inactive[
           Div][({{-\[Mu], 0}, {0, -\[Mu]}}.Inactive[Grad][
             v[x, y], {x, y}]), {x, y}] + v[x, y]/y^2 - 
         D[v[x, y], y]/y + Re1*(Abs[\[CapitalRho][i - 1][x, y]^q])*
\!\(\*SuperscriptBox[\(\[Rho]\), 
TagBox[
RowBox[{"(", 
RowBox[{"0", ",", "1"}], ")"}],
Derivative],
MultilineFunction->None]\)[x, y] + Re0*UX[i - 1][x, y]*D[v[x, y], x] +
          Re0*VY[i - 1][x, y]*D[v[x, y], y], 
        D[y*\[CapitalRho][i - 1][x, y]*u[x, y], x] + 
         D[y*\[CapitalRho][i - 1][x, y]*v[x, y], y]} == {0, 0, 
        0} /. \[Mu] -> 1, {
      DirichletCondition[{\[Rho][x, y] == 2, v[x, y] == 0}, x == 0.], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       0 <= x <= lc && y == rc || y == rp], 
      DirichletCondition[{u[x, y] == 0., v[x, y] == 0.}, 
       x == xp && rp <= y <= rc],
      DirichletCondition[{\[Rho][x, y] == 1, v[x, y] == 0}, x == lc], 
      DirichletCondition[v[x, y] == 0, y == h]}}, {u, 
     v, \[Rho]}, {x, y} \[Element] \[CapitalOmega], 
    Method -> {"FiniteElement", 
      "InterpolationOrder" -> {u -> 2, v -> 2, \[Rho] -> 1}, 
      "MeshOptions" -> {"MaxCellMeasure" -> 0.0005}}], {i, 1, K}];
StreamDensityPlot[{UX[K][x, y], 
  VY[K][x, y]}, {x, y} \[Element] \[CapitalOmega], 
 StreamPoints -> Fine, StreamStyle -> LightGray, 
 PlotLegends -> Automatic, VectorPoints -> Fine, 
 ColorFunction -> "TemperatureMap", FrameLabel -> {"x", "y"}]

{ContourPlot[\[CapitalRho][K][x, 
   y], {x, y} \[Element] \[CapitalOmega], PlotLegends -> Automatic, 
  Contours -> 20, PlotPoints -> 25, ColorFunction -> "TemperatureMap",
   AxesLabel -> {"x", "y"}, PlotLabel -> \[Rho]], 
 ContourPlot[
  Norm[{UX[K][x, y], VY[K][x, y]}]/\[CapitalRho][K][x, y]^(q/2), {x, 
    y} \[Element] \[CapitalOmega], PlotLegends -> Automatic, 
  Contours -> 20, PlotRange -> All, PlotPoints -> 50, 
  ColorFunction -> "TemperatureMap", AxesLabel -> {"x", "y"}, 
  PlotLabel -> "M"]}

In Fig. The distributions of the velocity, density and Mach number