How to make the boundaries thin and smooth of a binary image?

Question

Consider a binary image img as

How can I make the edges thin and smooth?

@Rahul Thanks, it works. Although the roughness is still there. — user36426, Feb 28 '18 at 10:51

score 6 · Answer 1 · answered Feb 28 '18 at 15:31

6

You can get it to be a little smoother by dilating before the thinning:

img = Import["https://i.stack.imgur.com/z0Vet.png"]
Thinning[Dilation[img, 1]]

answered Feb 28 '18 at 15:31

bill s

68,936
4
101
191

1

Just about any smoothing before thinning works:
Thinning[Binarize[GaussianFilter[img, 3]]] produces very similar results with maybe slightly smoother eyes.
– kjosborne Feb 28 '18 at 15:53

score 3 · Answer 2 · edited Jun 16 '20 at 09:23

3

Riding off Bill's answer, we can smooth further by upsampling with ImageMesh, thinning, then downsampling.

img = ImageCrop[Import["https://i.stack.imgur.com/z0Vet.png"]];
imsmall = Thinning[Dilation[img, 1]];
mesh = ImageMesh[imsmall, ImageSize -> 1200, 
  Background -> Black, BaseStyle -> White, Method -> "DualMarchingCubes"];
imlarge = Thinning[Dilation[Rasterize[mesh, "Image"], 12]];
res = Thinning[Binarize[ImageResize[imlarge, ImageDimensions[img]]]]

Edit

Notice one side of each feature boundary is fairly smooth. I exploit this with a very manual approach:

level1 = Thinning[EdgeDetect[FillingTransform[img]]];
level2 = Thinning[EdgeDetect[FillingTransform[Dilation[
  ImageDifference[img, GeodesicClosing[img, 14]], 1]]]];
level3 = Thinning[EdgeDetect[Dilation[
  ImageDifference[img, GeodesicClosing[img, 8]], 1]]];
res = level1 + level2 + level3

Dilation[res, 1]

edited Jun 16 '20 at 09:23

Community

1

answered Feb 28 '18 at 17:12

Greg Hurst

35,921
1
90
136

Is there any python implementation of this? – Bharath_Raja Apr 26 '20 at 18:55
Can you please help me with which language this is written? @Chip – Bharath_Raja Apr 26 '20 at 18:56
@Bharath_Raja https://www.wolfram.com/language/ – Greg Hurst Apr 26 '20 at 19:12
Where can I find the documentation and list of operations used in the above solution? – Bharath_Raja Apr 26 '20 at 19:27
Here’s an example. You can search for others on the same site. https://reference.wolfram.com/language/ref/Dilation.html – Greg Hurst Apr 26 '20 at 19:29

score 3 · Answer 3 · answered Feb 28 '18 at 19:32

Another idea is picking out the components and then approximating each component with a smooth spline. I tried with BSpline and Bezier, perhaps it can be used as a start.

img = Import["https://i.stack.imgur.com/z0Vet.png"];
components = MorphologicalComponents[img];
components // Colorize

Mathematica graphics

For example, one of the components can be approximated like this:

pts = RandomSample[Position[components, 2], 100];
{dist, order} = FindShortestTour[pts];
pts = Part[pts, order];
BSplineCurve[pts, SplineDegree -> 100] // Graphics

Mathematica graphics

The spline degree was chosen by experimenting. The shape is not a perfect circle, but it is rather smooth. Now we do the same for the rest of the components:

smoothComponent[comp_, splineType : "Bezier" | "BSpline"] := Module[{pts, dist, order},
  pts = RandomSample[Position[components, comp], 80];
  {dist, order} = FindShortestTour[pts];
  pts = Part[pts, order];
  If[
   splineType == "BSpline",
   BSplineCurve[pts, SplineDegree -> 100],
   BezierCurve[pts, SplineDegree -> 15]
   ]
  ]

bspline = smoothComponent[#, "BSpline"] & /@ Range[2, 9];
ImageRotate[Graphics[bspline], -90 Degree]

Mathematica graphics

bezier = smoothComponent[#, "Bezier"] & /@ Range[2, 9];
ImageRotate[Graphics[bezier], -90 Degree]

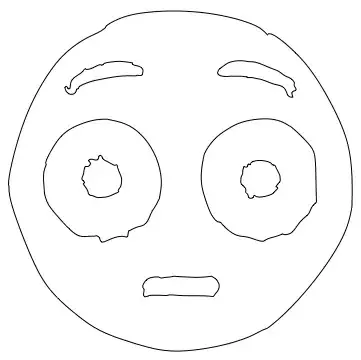
Mathematica graphics

Especially the Bezier curve didn't turn out that well. I mainly wanted to show this alternative type of answer, which is different from the image processing solutions so far.

Parameters to play with: How many points to sample from each component, and what the spline degree should be for the Bezier curve and BSpline respectively.

How to make the boundaries thin and smooth of a binary image?

3 Answers3

Edit

Linked