1

I'm trying to illustrate the generation of the conic curves with a plane and a cone surface in ContourPlot3D, when I make a static plane there is no problem, and the intersection curve was generated as in this documentation example, the code is:

Clear[h, g];
h = x^2 + y^2 - z^2;
g = z - 4;
ContourPlot3D[{h == 0, g == 0}, {x, -5, 5}, {y, -5, 5}, {z, -5, 5}, 
 MeshFunctions -> {Function[{x, y, z}, h - g]}, 
 MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}, 
 ContourStyle -> 
  Directive[Orange, Opacity[0.5], Specularity[White, 30]]]

Correct, but static, circumference of intersection

In order to make a dynamic view of the movement of the cut plane, I've tried with this code:

Clear[h, g];
h = x^2 + y^2 - z^2;
g = z - a;
Manipulate[
 ContourPlot3D[{h == 0, g == 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, 
  MeshFunctions -> {Function @@ Hold[{x, y, z}, h - g]}, 
  MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}, 
  ContourStyle -> 
   Directive[Orange, Opacity[0.5], Specularity[White, 30]]], {a, -1.8,
   1.8}]

But, get this error:

MeshFunctions::invmeshf: MeshFunctions->Function[{x,y,z},h-g] must be a pure function or a list of pure functions.

I've tried to Hold also the variable a of the Manipulate:

Clear[h, g, a];
h = x^2 + y^2 - z^2;
g = z - a;
Manipulate[
 ContourPlot3D[{h == 0, g == 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, 
  MeshFunctions -> {Function @@ Hold[{a, x, y, z}, h - g]}, 
  MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}, 
  ContourStyle -> 
   Directive[Orange, Opacity[0.5], Specularity[White, 30]]], {a, -1.8,
   1.8}]

and get now this error:

MeshFunctions::invmeshf: MeshFunctions->Function[{FE`a$$445,x,y,z},h-g] must be a pure function or a list of pure functions.

I don't know if I need to use ReleaseHold in some part of the code.

I've tried also with this question, obtaining a code like this:

cutplane := z - a;

SetAttributes[surface, HoldFirst]


surface[c_] := 
 ContourPlot3D[{x^2 + y^2 - z^2 == 0, c == 0}, {x, -1, 1}, {y, -1, 
   1}, {z, -1, 1}, 
  MeshFunctions -> 
   Function @@ Hold[{a, x, y, z}, x^2 + y^2 - z^2 - c], 
  MeshStyle -> {{Thick, Black}}, Mesh -> {{0}}, 
  ContourStyle -> {Opacity[0.9], None}, BoundaryStyle -> None]


Manipulate[surface[cutplane], {a, -1, 1}]

But, I've obtained a figure like this that doesn't change.

Another option that hasn't worked

How can I get a dynamic animation that shows this circumference intersections of the cone and plane?

Community
  • 1
Benjamin Luna
  • 11
  • 1
  • 3
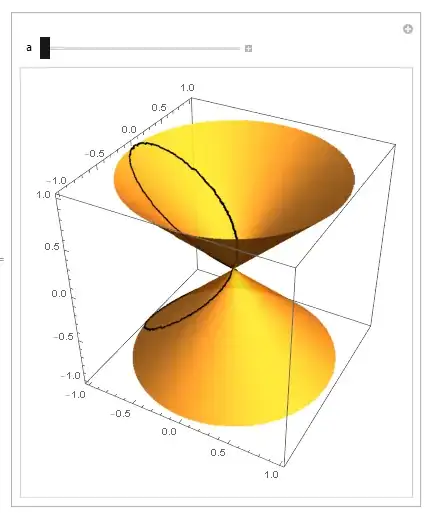
    Put the functions inside: Manipulate[ContourPlot3D[{x^2 + y^2 - z^2 == 0, z - a == 0}, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, MeshFunctions -> {Function[{x, y, z}, (x^2 + y^2 - z^2) - (z - a)]}, MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}, ContourStyle -> Directive[Orange, Opacity[0.5], Specularity[White, 30]]], {a, -1.8, 1.8}]. The a inside the Manipulate[] is a different symbol from the a in the expressions defined outside it. – J. M.'s missing motivation Mar 04 '18 at 03:02
  • Thank you so much, it works well. Is there any form of declare the functions outside? – Benjamin Luna Mar 04 '18 at 03:14
  • Linked topic should address the essence of your question but let me know if you, or anyone disagree. – Kuba Mar 04 '18 at 05:56

1 Answers1

2

Turning J.M.'s comment and your comment into an answer, this is one of many, many ways to declare the function outside of the Manipulate

surf[a_] :=
 ContourPlot3D[
  {x^2 + y^2 - z^2 == 0, z - a == 0},
  {x, -2, 2}, {y, -2, 2}, {z, -2, 2},
  MeshFunctions ->
   {Function[{x, y, z}, (x^2 + y^2 - z^2) - (z - a)]}, 
  MeshStyle -> {{Thick, Blue}}, Mesh -> {{0}}, 
  ContourStyle -> 
   Directive[Orange, Opacity[0.5], Specularity[White, 30]]
  ]

Manipulate[
 surf[a], {a, -1.8, 1.8}
 ]
b3m2a1
  • 46,870
  • 3
  • 92
  • 239