2

I am trying to redo the method given in

Solving a simple BVP

which is very nice, to my equation 

2 + 2 u'[x2]^2 + u[x2] u''[x2]

where x2=[-1.,1.] and u[-1.]=u[1.]=1/10. I copyed the steps and change the pamareters, obviously. My code in this case is

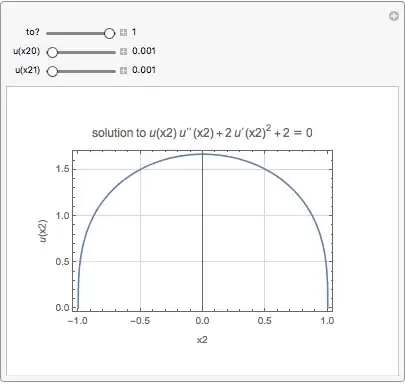
Manipulate[eq = 2 + 2 u'[x2]^2 + u[x2] u''[x2] == 0;
 ic = {u[-1] == ic0, u[1] == ic1};
 sol = First@NDSolve[Flatten[{eq, ic}], u[x2], {x2, -1, to}];
 Plot[u[x2] /. sol, {x2, -1, to}, Frame -> True, PlotRange -> All, 
  ImagePadding -> 50, 
  FrameLabel -> {{u[x2], None}, {x2, 
     Style[Row[{"solution to ", 
        2 + 2 Derivative[1][u][x2]^2 + 
          u[x2] (u^\[Prime]\[Prime])[x2] == 0}], 12]}}, 
  GridLines -> Automatic, 
  GridLinesStyle -> Directive[LightGray, Thickness[.001]]], {{to, 1, 
   "to?"}, 0, 1, .01, ImageSize -> Tiny, 
  Appearance -> "Labeled"}, {{ic0, 1/10, "u(x20)"}, 0, 1, .01, 
  ImageSize -> Tiny, Appearance -> "Labeled"}, {{ic1, 1/10, "u(x21)"},
   0, 1, .01, ImageSize -> Tiny, Appearance -> "Labeled"}]

As a result, I get

Power::infy: Infinite expression 1/0. encountered.

Power::infy: Infinite expression 1/0.^2 encountered.

Power::infy: Infinite expression 1/0. encountered.

General::stop: Further output of Power::infy will be suppressed during this calculation.

Infinity::indet: Indeterminate expression 0. ComplexInfinity encountered.

Infinity::indet: Indeterminate expression 0. ComplexInfinity encountered.

NDSolve::ndnum: Encountered non-numerical value for a derivative at x2 == -1..

and

ReplaceAll::reps: {2+2 (u^[Prime])[-0.999959]^2+u[-0.999959] (u^[Prime][Prime])[-0.999959]==0,u[-1]==1/10,u1==1/10} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing.

ReplaceAll::reps: {2. +2. (u^[Prime])[-0.999959]^2+u[-0.999959] (u^[Prime][Prime])[-0.999959]==0.,u[-1.]==0.1,u[1.]==0.1} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing.

ReplaceAll::reps: {2+2 (u^[Prime])[-0.959143]^2+u[-0.959143] (u^[Prime][Prime])[-0.959143]==0,u[-1]==1/10,u1==1/10} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing.

General::stop: Further output of ReplaceAll::reps will be suppressed during this calculation.

I ask the same question giving my whole code and parameters in

My code

where you can see that u[-1.]=u[1.]=1/100, but thats not the main point.

Michael E2
  • 235,386
  • 17
  • 334
  • 747
Patrick El Pollo
  • 593
  • 3
  • 12

1 Answers1

3

The automatic Shooting Method does not suffer errors well. It seems to give up when poorly chosen initial conditions lead to an error. In this case, there is a lower limit on the initial condition for u'[-1], below which the solution develops a singularity. It is very close to the actual solution, so the built-in shooting method inevitably runs into a singularity and fails. Thus a manual approach seems to be necessary. We add an extrapolation handler that will cause FindRoot to increase the initial condition when this happens.

Also, one cannot have boundary conditions u[-1] == 0 nor u[1] == 0, since in solving for u''[x2], the equation is divided by u[x2]. So I limited the input range on the sliders for the BCs.

Manipulate[
 eq = 2 + 2 u'[x2]^2 + u[x2] u''[x2] == 0;
 ic = {u[-1] == ic0, u[1] == ic1};
 With[{pen = 3/ic0^2},   (* slightly informed guess *)
  psol = ParametricNDSolveValue[
    Flatten[{eq, {u[-1] == ic0, u'[-1] == p0}}], u, {x2, -1, 1}, {p0},
     "ExtrapolationHandler" -> {p0 - pen &, "WarningMessage" -> False}]
  ];
 Quiet[
  usol = psol[p0] /. FindRoot[psol[p0][1] == ic1,
     {p0, 2/ic0^2, E/ic0^2}],  (* starting values from inspection of psol *)
  ParametricNDSolveValue::ndsz];
 Dynamic@Plot[usol[x2], {x2, -1, to}, Frame -> True, 
   PlotRange -> {{-1, 1}, All}, PlotRangePadding -> Scaled[.02], 
   ImagePadding -> 50, 
   FrameLabel -> {{u[x2], None}, {x2, 
      Style[Row[{"solution to ", 
         2 + 2 u'[x2]^2 + u[x2] u''[x2] == 0}], 12]}}, 
   GridLines -> Automatic, 
   GridLinesStyle -> Directive[LightGray, Thickness[.001]]],
 {{to, 1, "to?"}, 0, 1, .01, ImageSize -> Tiny, Appearance -> "Labeled"},
 {{ic0, 1/10, "u(x20)"}, 0.001, 1, .01, ImageSize -> Tiny, Appearance -> "Labeled"},
 {{ic1, 1/10, "u(x21)"}, 0.001, 1, .01, ImageSize -> Tiny, Appearance -> "Labeled"}]

Mathematica graphics

usol'[-1]  (*  p0  found by FindRoot for  ic0 = 0.001  is approx  E/ic0^2 *)
(*  2.78641*10^6  *)

Note how large the derivative is compared to the size of the solution. It might be hard to lower the limit on the slider for ic0, without increasing precision.

Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Thanks for your answer. I'd like to ask how did you get those values for p0, [p0, 2/ic0^2, E/ic0^2]? – Patrick El Pollo Mar 12 '18 at 11:38
  • Another doubt, how did you get that "slightly informed guess" for pen? – Patrick El Pollo Mar 12 '18 at 12:06
  • 1
    For p0, when I got the answer for ic0 = 0.1, I thought p0 is about 100 or so, or about 1/ic0^2 (it was actually 200+, so 2/ic0^2). I solved it for ic0 = 0.01 and again it was about 2/ic0^2. The second point was originally 1/ic0^2, which worked, but I realized that all the solutions I saw were about 2.7 or 2.8 times 1/ic0^2. For the penatly pen, I picked a number that was bigger than that. The value returned will be negative when p0 is too small and integration did not make it to x2 == 1; since ic1 > 0, the secant method will then increase p0 on the next step. – Michael E2 Mar 12 '18 at 13:11
  • How did you solved for ic0=0.1 or ic0=0.01 to confirm that p0 goes like 1/ic0^2? Why did you expect that in principle? – Patrick El Pollo Mar 13 '18 at 18:10
  • 1
    @resanrom For an initial value for u'[-1] in the IVP, pick successively things like 1, 10, 100, etc. and examine the solution, what it looks like, and how close to the BC at 1 you get. One could do that inside Manipulate, too and adjust the IC with a slider. As for "in principle," I just guessed, from two data points, maybe more. I forget. I didn't have time to do the analysis; maybe someone else can. (Actually, all I could see from the calculations, is that it's close enough a guess for FindRoot to succeed, which I verified by moving the slider.) – Michael E2 Mar 13 '18 at 22:10
  • I was trying to find details about ExtrapolationHandler, and I only found your answer here. In particular, here, you write "ExtrapolationHandler" -> {p0 - pen &, "WarningMessage" -> False} inside ParametricNDSolveValue. I didnt understand very well this line, why do I need to stablish a penalty? What does mean "WarningMessage" -> False}? – Patrick El Pollo Apr 05 '18 at 23:57
  • Also, p0 - pen in this Extrapolationshandler imposes some kind of contidion in the solution? – Patrick El Pollo Apr 06 '18 at 00:13
  • 1
    @resanrom I learned of "ExtrapolationHandler" here. Extrapolation is what happens when the input to an interpolating function lies outside the domain. The handler is a function that is applied to such an input. Normally, a warning message is issued, but that can be turned off. A penalty is a common method to enforce a constraint when solving an equation. In this case, extrapolation happens when the integration did not reach the end at x2 == 1; the penalty indicates the – Michael E2 Apr 06 '18 at 00:45
  • 1
    parameter caused the solution to evaluate to a value <= p0. If the integration completed (reached x2 == 1) the boundary value will be >= p0. The desired value of the parameter will be between those two values, unless in the first case, the solution improbably evaluates exactly to p0. – Michael E2 Apr 06 '18 at 00:47
  • I saw it is an amazing tool. Let me try to define with you what ExtrapolationHandler does in general. In general, then, ExtrapolationHandler is written as "ExtrapolationHandler" -> {extra &, "WarningMesage" -> False}, where extra is the value of the interpolation function when we ask point outside the obtained domain, right?, and "WarningMessage" ->False that turns off the message that tells you are outside the domain, I got that. – Patrick El Pollo Apr 06 '18 at 22:19
  • When you ask for a value that it is outside the domain, you replace the Interpolate function with extra, right? As is said here with extra as Indeterminate. – Patrick El Pollo Apr 06 '18 at 22:19
  • When I played with the program, a simplified one, in which I suppress the Dynamic part. I separate a bit more x20 and x21, then pen=3/u0^2 leads to p0=pen as the solution. Does it mean that extra in ExtrapolationHandler must be zero? – Patrick El Pollo Apr 06 '18 at 22:26
  • Sorry if these lines of comments became too large, and if there is a rule here that tells you must delete large lines of comments, I will try to write a nice definition of ExtrapolationHandler below my question for future references. – Patrick El Pollo Apr 06 '18 at 22:28
  • @resanrom Your general idea about ExtrapolationHandler is right. The only rule I know is that comments are not for long discussions like this. – Michael E2 Apr 07 '18 at 13:17
  • I agree. But I think this discussion is in some way useful for people looking for datails about ExtrapolationHandler. Moreover, since ÈxtrapolationHandler allow us to aplly the penaly method, is it possible to do it for a system of coupled PDEs? I mean, something like "ExtrapolationHandler"->{{penalty1,penalty2,...}&, "WarningMessage"->False}. – Patrick El Pollo Apr 12 '18 at 14:06