N[Sum[1/(x^2 + 1), {x, 1, Infinity}], 5]
N[Sum[1/(x^2 + x + 1), {x, 1, Infinity}], 5]
1.0767
0.79815 + 0.*10^-6 I
What causes the strange number?
N[Sum[1/(x^2 + 1), {x, 1, Infinity}], 5]
N[Sum[1/(x^2 + x + 1), {x, 1, Infinity}], 5]
1.0767
0.79815 + 0.*10^-6 I
What causes the strange number?
Note that Mathematica can do the symbolic sums:
Sum[1/(x^2 + 1), {x, 1, Infinity}]
gives
$$ \frac{1}{2} (-1 + \pi \coth[\pi]) $$
and
Sum[1/(x^2 + x + 1), {x, 1, Infinity}]
gives
$$
-\frac{i \left(\psi ^{(0)}\left(1+\sqrt[3]{-1}\right)-\psi ^{(0)}\left(1-(-1)^{2/3}\right)\right)}{\sqrt{3}}
$$
(where $\psi^{(0)}(x)$ is PolyGamma[0,x], and in fact if you apply FullSimplify this can be written in terms of HarmonicNumber as well). But you are asking for numeric versions of these to a specific number of significant figures. To that precision, the imaginary parts of the latter function do not quite cancel, and hence you get a small imaginary part.
Note also that using NSum[...] instead of N[Sum[...]] works better here, since it actually does the numerical sum by adding the terms, as opposed to calculating the symbolic form and then numerically evaluating it.
Sum can't solve the sum symbolically (not applicable here), N[Sum[...] seems to be equivalent to NSum[...] according to the docs for NSum.
– Jens
Dec 22 '12 at 17:31
Mathematica 8 and 9.
– Artes
Feb 04 '13 at 20:04
There are several methods in Sum which may help in various cases. To find your second sum symbolically in apparently real form you can try, e.g.
Sum[1/(1 + x + x^2), {x, 1, Infinity}, Method -> "HypergeometricTermPFQ"]
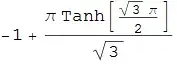
However there are still other ways to get the same result without methods specified, e.g. :
s = Sum[1/(1 + x + x^2), {x, 1, Infinity}];
FullSimplify[ ComplexExpand //@ s ]
or
FullSimplify @ ExpToTrig @ s
Note that we had to MapAll (shorthand //@) ComplexExpand i.e. apply the latter to every subexpression of s