6

I am plotting three surfaces on a 3D plot. They differ in the value of one parameter. Is there a way to distinguish each surface for various values of the parameter?

My code is:

Plot3D[{
  2*(Cosh[ h/ T]*(2 + Exp[2    / T]) + Exp[-2     / T]*Cosh[3 h/ T] ), 
  2*(Cosh[ h/ T]*(2 + Exp[2  10/ T]) + Exp[-2   10/ T]*Cosh[3 h/ T] ), 
  2*(Cosh[ h/ T]*(2 + Exp[2 100/ T]) + Exp[-2  100/ T]*Cosh[3 h/ T] )},
  {T, 0.001, 1000},
  {h, 0, 1}, 
  PlotLabel -> Style[Framed["Partition Function Z"], 20, Red, 
    Background -> Lighter[LightYellow]],
  Background -> LightGray, 
  ColorFunction -> "BlueGreenYellow", 
  AxesLabel -> {T[kelvin], B[tesla]},
  BoundaryStyle -> Thick, 
  ClippingStyle -> Opacity[0.5]]

The output graphics is:

enter image description here

EDIT

I am trying to use ShowLegend because PlotLegend cannot work with Plot3D in v8... The code I am using is:

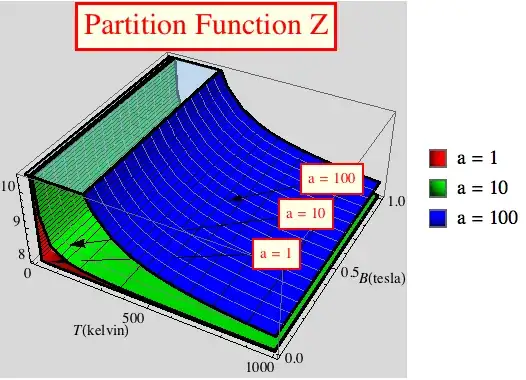
Z[T_, h_, a_] := 2*(Cosh[h/T]*(2 + Exp[2 a/(T)]) + Exp[-2/(T)]*Cosh[3 h/T]);
params = {1, 10, 100};
ShowLegend[
  Plot3D[
    Evaluate[Table[Tooltip[Z[T, h, a], StringForm["a = ``", a]], {a, params}]],
    {T, 0.001, 1000},
    {h, 0, 1}, 
    PlotLabel -> Style[Framed["Partition Function Z"], 20, Red, 
      Background -> Lighter[LightYellow]], 
    MeshFunctions -> {(*#1&,*)#2 &, #3 &}, 
    Mesh -> {(*15,*)15, Range[7.5, 11, 0.1]}, 
    MeshStyle -> {(*Gray,*)Gray, Black}, Background -> LightGray, 
    PlotStyle -> {Red, Green, Blue},
    (*PlotLegends->Table[StringForm["a = ``",a],{a,params}],*)
    AxesLabel -> {T[kelvin], B[tesla]}, 
    BoundaryStyle -> Thick,
    ClippingStyle -> Opacity[0.5]], 
  Graphics3D[{
    Table[{Arrowheads[0.0004], 
      Arrow[{{900, 0.2 + 0.25 Log10[a], 9.5},
        {50. + 5 a, 0.01 + 0.005 a, Z[50. + 5 a, 0.01 + 0.005 a, a]}}], 
      Text[Style[Framed[StringForm["J = ``", a]], Red, Background -> Lighter[LightYellow]],
        {900, 0.2 + 0.25 Log10[a], 9.5}]},
      {a, params}]}],
  {{{Graphics[{Table[StringForm["a = ``", a], {a, params}]}]}}, 
    LegendPosition -> {1.1, -.4}}]
Adrian
  • 411
  • 4
  • 14
Thanos
  • 1,003
  • 1
  • 12
  • 21
  • It's in the documentation, isn't it? "Provide separate styles for different surfaces: PlotStyle -> {Red, Blue}". You'll want to provide three colours, get rid of ColorFunction, and use Lighting -> "Neutral". –  Dec 26 '12 at 11:39
  • @RahulNarain: Thank you very much for your comment. The thing is that I don't need just one colour on each surface, but actually a gradient illustrating height. – Thanos Dec 26 '12 at 11:47
  • Probably easiest to generate each plot separately using a different ColorFunction for each; then use Show to combine the three images. – Mark McClure Dec 26 '12 at 12:27
  • @MarkMcClure: Thank you very much for your suggestion. In that way, though will I be able to use a legend? – Thanos Dec 26 '12 at 12:29
  • Your ShowLegend syntax is a little off. Wrap Plot3D and Graphics3D in Show[..] so that it is a single argument -- or you might drop the arrows if you're going to use a legend. Then the second argument should be something like {Table[{Graphics[{{Red, Green, Blue}[[1 + Log10[a]]], Rectangle[]}], StringForm["J = ``", a]}, {a, params}], LegendPosition -> {1.1, -.4}}. See belisarius's edit for another way, which preserves 3d interactivity. – Michael E2 Dec 27 '12 at 16:42

2 Answers2

9
f[k_, h_, t_] := 2*(Cosh[h/t]*(2 + Exp[(2/t) 10^k]) + Exp[-(2 /t) 10^k]*Cosh[3 h/t]);

grad = {"LakeColors", "DarkRainbow", "NeonColors"};

Show@Table[
  Plot3D[f[k, h, t], {t, 0.001, 1000}, {h, 0, 1}, 
   ColorFunction -> grad[[k + 1]], ColorFunctionScaling -> True, 
   PlotRange -> {8, 8.8},
   PlotLabel -> Style[Framed["Partition Function Z"], 20, Red, Background -> Lighter[LightYellow]], 
   Background -> LightGray, AxesLabel -> {T[kelvin], B[tesla]}, BoundaryStyle -> Thick, 
   ClippingStyle -> Opacity[0.5]
   ], {k, {0, 1, 2}}]

Mathematica graphics

Edit

Or you could do something like this:

f[k_, h_, t_] := 2*(Cosh[h/t]*(2 + Exp[(2/t) 10^k]) + Exp[-(2/t) 10^k]*Cosh[3 h/t]);

Needs["PlotLegends`"];
GraphicsRow[{
 Show@Table[Plot3D[f[k, h, t], {t, 0.001, 1000}, {h, 0, 1},
     ColorFunction -> 
      Function[{x,y,z}, RGBColor[Sequence @@ RotateLeft[{1,0,0}, k], Rescale[z, {7.8,8.8}]]],
     ColorFunctionScaling -> False,
     MeshFunctions -> {#3 &},
     PlotRange -> {8, 8.8},
     PlotLabel -> Style[Framed["Partition Function Z"], 20, Red],
     Background -> LightGray,
     AxesLabel -> {T[kelvin], B[tesla]},
     BoundaryStyle -> Thick,
     ClippingStyle -> Opacity[0.5]],
    {k, {0, 1, 2}}],
  Graphics@
   Legend[
      Table[{Graphics[{RGBColor[Sequence @@ RotateLeft[{1, 0, 0}, k]], Rectangle[]}], 10^k}, 
      {k, 0, 2}], LegendBorder -> None, LegendShadow -> None]}]

Mathematica graphics

Dr. belisarius
  • 115,881
  • 13
  • 203
  • 453
5

There are various things you might try, depending on your particular objectives.

  1. If you aren't wedded to gradients, you can use #3& as a mesh function to indicate height. For your particular functions, you might wish to omit #1& as a mesh function, since the mesh lines are parallel.

  2. If you need to distinguish graphs in an notebook and not in a printout, you can use tooltips.

  3. You can insert 3D graphics to draw labels & arrows to the plots. Possibly unsatisfactory if the graph is to be rotated about.

Here is an example incorporating all three ideas (with belisarius's label).

Z[T_, h_, a_] := 
  2*(Cosh[h/T]*(2 + Exp[2 a/(T)]) + Exp[-2/(T)]*Cosh[3 h/T]);
params = {1, 10, 100};
Show[Plot3D[
  Evaluate[Table[
    Tooltip[Z[T, h, a], StringForm["a = ``", a]], {a, params}]], {T, 
   0.001, 1000}, {h, 0, 1}, 
  PlotLabel -> 
   Style[Framed["Partition Function Z"], 20, Red, 
    Background -> Lighter[LightYellow]], 
  MeshFunctions -> {(*#1&,*)#2 &, #3 &}, 
  Mesh -> {(*15,*)15, Range[7.5, 11, 0.1]}, 
  MeshStyle -> {(*Gray,*)Gray, Black}, Background -> LightGray, 
  PlotStyle -> {Red, Green, Blue}, 
  PlotLegends -> Table[StringForm["a = ``", a], {a, params}], 
  AxesLabel -> {T[kelvin], B[tesla]}, BoundaryStyle -> Thick, 
  ClippingStyle -> Opacity[0.5]],
 Graphics3D[{Table[{Arrowheads[0.0004], 
     Arrow[{{900, 0.2 + 0.25 Log10[a], 9.5}, {50. + 5 a, 
        0.01 + 0.005 a, Z[50. + 5 a, 0.01 + 0.005 a, a]}}], 
     Text[Style[Framed[StringForm["a = ``", a]], Red, 
       Background -> Lighter[LightYellow]], {900, 0.2 + 0.25 Log10[a],
        9.5}]}, {a, params}]}]
 ]

Output from example

Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • Thank you very much for your answer! The thing is that I use v8.0.0, which means that PlotLegend isn't working. But that's not my problem. I commented PlotLegends -> Table[StringForm["a = ``", a], {a, params}] and run the rest but I got 2 errors...http://i.imgur.com/uOXNa.png AND http://i.imgur.com/2W8Nx.png – Thanos Dec 27 '12 at 07:31
  • After the PlotStyle option, you have to commas in a row, which translates to a Null. The commas are likely on either side of the PlotLegends option, which you commented out -- include one of the commas in the comment or delete it. That should cure the second error, too. – Michael E2 Dec 27 '12 at 16:08
  • By the way, there is a PlotLegends package in v8. – Michael E2 Dec 27 '12 at 16:14
  • You were right about the comma...Silly me! As far as PlotLegend is concerned, I was dealing with a similar problem and I was suggested to use ShowLegend[Plot3d[...],{{{Graphics[...],...}}}] because in v8 PlotLegend cannot work with Plot3D... The thing is that I cannot get it to work... Check my edited question for the code... – Thanos Dec 27 '12 at 16:18