Symbolic solution to a constrained optimization problem

Question

Can anyone tell me why this method (Symbolic Constrained Optimization) works but not the following for obtaining symbolic solutions of a constrained optimization problem:

MaxValue[{a^(1/2)*(y - p*q)^(1/2) + d*(1/2)*(Q + q - a), 
  a <= Q + q &&  q <= y/p &&  q >= 0 &&  a >= 0}, {a, q}]

But it freezes, so I assign some values to the parameters:

y = 50
p = 2
d = 0.95
MaxValue[{a^(1/2)*(y - p*q)^(1/2) + d*(1/2)*(Q + q - a), 
  a <= Q + q &&  q <= y/p &&  q >= 0 &&  a >= 0}, {a, q}]

Out = MaxValue[{Sqrt[a] Sqrt[50 - 2 q] + 0.475 (-a + q + Q), 
  a <= q + Q && q <= 25 && q >= 0 && a >= 0}, {a, q}]

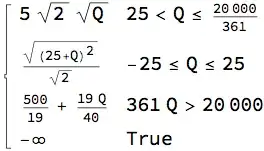
I guess that the square roots are the main obstruction for using symbolic optimization. In the second example, Q still has no numerical value assigned. — Henrik Schumacher, Mar 25 '18 at 18:55

score 1 · Accepted Answer · answered Mar 25 '18 at 19:14

Use an exact value for d (or Rationalize)

$Version

(* "11.3.0 for Mac OS X x86 (64-bit) (March 7, 2018)" *)

y = 50;
p = 2;
d = 95/100;

f[Q_] = MaxValue[{a^(1/2)*(y - p*q)^(1/2) + d*(1/2)*(Q + q - a), a <= Q + q, 
   q <= y/p, q >= 0, a >= 0}, {a, q}]//Simplify

Plot[f[Q], {Q, -50, 100}]

Symbolic solution to a constrained optimization problem

1 Answers1