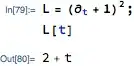How to define a differential operator in Mathematica?

Question

I want to define an operator $(\partial_{t}+1)^{2}=\partial_{t}\partial_{t}+2\partial_{t}+1$. Then, I want it to act on $t$. My code looks like this:

op[t_] := (D[#, {t, 1}] + 1 #)^2 &
op[t][t]

Instead of giving $2+t$, its result is $(1+t)^{2}.$ To verify if $2+t$ is really the answer, I write the right-hand side of the operator in Mathematica. My code looks like this:

op[t_] := (D[#, {t, 2}] + 2*D[#, {t, 1}] + 1 #) &
op[t][t]

And, it gives $2+t$. I want to write the exponent explicitly because I plan to extend it to $5$ (instead of $2$), and act it on another function. Can someone help me on this? Thank you.

$(\partial_{t}+1)^{2}t=(\partial_{t}^{2}+2\partial_{t}+1)t= (\partial_{t}^{2}t+2\partial_{t}t+t)=(2+t)$ — RaymartJay, Mar 27 '18 at 07:03
@CarlWoll, I actuallly referred to How to define a differential operator?, but, still, my operator does not give the correct answer. — RaymartJay, Mar 27 '18 at 07:07
What is meant by "act it on another function" and "act on" (in this context)? — Peter Mortensen, Mar 27 '18 at 13:00
@PeterMortensen, what I meant by "act on" is the usual operation done by a differential operator on a function. And "act it on another function" means using another function instead of the function t. I hope this clarifies your question. — RaymartJay, Mar 27 '18 at 14:16

Carl Woll · Answer 1 · 2018-03-27T16:49:19.083

7

(From my answer to the linked question)

Install the DifferentialOperator paclet with:

PacletInstall["https://github.com/carlwoll/DifferentialOperator/releases/download/0.1/DifferentialOperator-0.0.1.paclet"]

and load with:

<<DifferentialOperator`

The paclet defines an input auto replacement for a special partial character, which you must use instead of the normal \[Partial] character. Specifically, you must enter pd and not EscpdEsc. Then, you can define a differential operator and apply it to a function as follows:

edited Mar 27 '18 at 16:49

answered Mar 27 '18 at 07:08

Carl Woll

130,679
6
243
355

Thank you. But, I don' understand why I get $0[t]$ instead of $2+t$. – RaymartJay Mar 27 '18 at 07:24
@RaymartJay Assuming you loaded my paclet, then you should use pd, not esc pd esc to enter the partial symbol. – Carl Woll Mar 27 '18 at 07:28
@CarlWoll, I am using your paclet for a project of mine and I am wondering if you put a built in function to make a change of variable in the differential operators ? – Ezareth Jul 17 '18 at 10:27
It's not clear how to enter the pd command – NC520 Dec 01 '22 at 00:33

ulvi · Accepted Answer · 2018-03-27T07:08:13.083

3

You want to use composition, not powers:

op := (D[#, {t, 1}] + #) &

op[t]

Out[86]= 1 + t

op[op[t]]

Out[87]= 2 + t

Composition[op, op]@t

Out[97]= 2 + t

Apply[Composition, Table[op, 5]]@(t^5)

Out[99]= 120 + 600 t + 600 t^2 + 200 t^3 + 25 t^4 + t^5

Expand[(x + 1)^5]

Out[101]= 1 + 5 x + 10 x^2 + 10 x^3 + 5 x^4 + x^5

edited Mar 27 '18 at 07:08

answered Mar 27 '18 at 07:00

ulvi

1,808
10
15

1

Off topcic note: to play with it one needs to copy it and manually drop/delete In[85] and friends. Consider not pasting them and insert output as e.g. commented code or quoted block (>) – Kuba Mar 27 '18 at 07:05
Thank you. I think this is better. – RaymartJay Mar 27 '18 at 07:21

How to define a differential operator in Mathematica?

2 Answers2