DirichletCondition in NDSolve causes asymmetry (Finite Element Method)

Question

Edit

Thanks for the responses. I now agree with xzczd and Bill Watts who kindly gave answers and user21 who wrote useful comments. Both my cases below are correct. On reflection I think I made an elementary mistake. I noted the need to give a Dirichlet Condition for the u-direction to provide a reference for displacements. I should have just tied down one point using the condition

 DirichletCondition[u[x, y] == 0, x == 0 && y == 0]

Instead I wrote

DirichletCondition[u[x, y] == 0, x == 0]

This latter condition fixes the entire edge y == 0. Fixing this edge introduces asymmetry. I apologise if I have caused pointless concerns. I have also added the single point DirichletCondition as Case 3 below. This gives the same result as Case 1 but fixes a starting point. Thanks to all that helped.

Original Question

If a DirichletCondition is not specified in NDSolve then a warning is given. However, if I specify a condition then I seem to get the wrong answer. Below I have Case 1 where I get the warning and then Case 2 where I don't but I think the answer is wrong. Here is a minimum working example involving a stress computation. We need the following code

Needs["NDSolve`FEM`"]
ClearAll[planeStress]; 
planeStress[
  Y_, ν_] := {Inactive[
     Div][{{-(Y/(1 - ν^2)), 
       0}, {0, -((Y*(1 - ν))/(2*(1 - ν^2)))}} . 
     Inactive[Grad][u[x, y], {x, y}], {x, y}] + 
       Inactive[
     Div][{{0, -((Y*ν)/(1 - ν^2))}, {-((Y*(1 - ν))/(2*(1 \
- ν^2))), 0}} . Inactive[Grad][v[x, y], {x, y}], {x, y}], 
     Inactive[
     Div][{{0, -((Y*(1 - ν))/(2*(1 - ν^2)))}, {-((Y*ν)/(1 \
- ν^2)), 0}} . Inactive[Grad][u[x, y], {x, y}], {x, y}] + 
       Inactive[
     Div][{{-((Y*(1 - ν))/(2*(1 - ν^2))), 
       0}, {0, -(Y/(1 - ν^2))}} . 
     Inactive[Grad][v[x, y], {x, y}], {x, y}]}

Case 1. I make a rectangular grid and apply a force to part of the top surface. The bottom is prevented from moving vertically and is free horizontally. There are no other horizontal forces or constraints.

L = 1; (* Length *)
h = 0.2; (* Height *)
Y = 20 10^10;(* Modulus of elasticity *)
ν = 33/100 ;(* Poission ratio *)
stress = 100;
mesh = ToElementMesh[Rectangle[{0, 0}, {L, h}]];
mesh["Wireframe"]

Now the solver

{uif, vif} = NDSolveValue[{
    planeStress[Y, ν] == {0, 
      NeumannValue[-stress, L/4 <=  x <= 3 L/4 && y == h]},

    DirichletCondition[v[x, y] == 0, 0 <=  x <=  L && y == 0]
    },
        {u, v}, Element[{x, y}, mesh]];

I get the message

NDSolveValue::femibcnd: No DirichletCondition or Robin-type NeumannValue was specified for {u}; the result may not be unique.

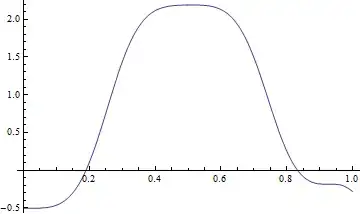
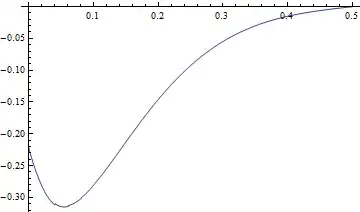
The results are good if I Plotthe horizontal displacement along the bottom edge I get

Plot[uif[x, 0], {x, 0, L}]

This has an arbitrary starting point but appears good and retains the symmetry of the problem. To test further I check the derivative (which I need to calculate the stress) and see if the left and right side are similar

du = Head@D[uif[x, y], x];
Plot[du[x, 0], {x, 0, L}]
Plot[du[x, 0] - du[L - x, 0], {x, 0, L/2}]

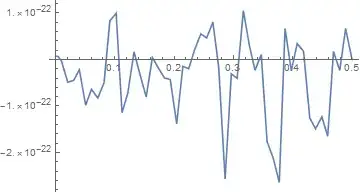
So far so good. I have a symmetric solution which is very good with the left and right sides differing only by numerical noise. However, I do have an arbitrary starting point for the horizontal displacement.

Case2. Now I try and fix the starting point for horizontal displacements by giving an additional DirichletCondition at one end of the mesh.

{uif, vif} = NDSolveValue[{
    planeStress[Y, ν] == {0, 
      NeumannValue[-stress, L/4 <=  x <= 3 L/4 && y == h]},

    DirichletCondition[v[x, y] == 0, 0 <=  x <=  L && y == 0],
     DirichletCondition[u[x, y] == 0, x == 0]
    },
        {u, v}, Element[{x, y}, mesh]];

This is where everything begins to go wrong. Plotting the displacement along the bottom edge gives

Plot[uif[x, 0], {x, 0, L}]

This starts from zero. Checking the derivative again I see problems

du = Head@D[uif[x, y], x];
Plot[du[x, 0], {x, 0, L}]
Plot[du[x, 0] - du[L - x, 0], {x, 0, L/2}]

Now there is a clear distortion and the left and right hand sides are not symmetric. What has gone wrong? Is there a workaround so that I can fix the location of the start of the displacements? Thanks

Edit

In the comments user21 suggests that in the second case the Dirichlet condition is applied to just one side so that this is an asymmetric case automatically. However, on physical grounds I think the symmetry should still be there particularly in the derivatives (the stresses).

Only vertical forces are applied. There are horizontal displacements due to the Poisson Ratio effect. This will cause the horizontal length of the block to increase. When considering stresses this effect will be symmetric. All this is confirmed in Case 1. When we come to Case 2 then when the Poisson Ratio expansion occurs the expansion to the left is prevented by the stop there. However, there are no other horizontal constraints so the block should push against the stop and all the expansion should be to the right. Thus in Case 2 the displacements should be the same as in Case 1 except for everything moving to the right. The derivatives on the left and right (the stresses) should just be the same. This is an argument from the physical stress analysis viewpoint. From the numerical viewpoint I think a constant should be added to the displacements. I suspect a gradient is being added to the displacements. I am surprised that in the first case there is a solution at all since there is nothing to tie down the system. I hope that adds some more background.

Edit 2 User xzczd has asked for the boundary condition in math notation. What I want is to define the stress on the upper surface. Thus

$$ 100 = \sigma_{yy} = \frac{E}{1 - \nu^2} (\frac{\partial v(x, y)}{\partial y} + \nu \frac{\partial u(x, y)}{\partial x})$$

for $ 1/4 < x < 3/4 $ and $ y = 0.2$.

Here $\sigma_{yy}$ is the stress in the vertical direction. I have the stress going downwards so this may be -σyy depending on the sign convention for the boundary. Also modulus of elasticity $E$ and Poisson Ratio $ν$ are E = 20 *10^10 and ν =0.33

** Edit and Case 3**

One point at x = 0 and y = 0 fixed.

{uif, vif} = NDSolveValue[{
    planeStress[Y, ν] == {0, 
      NeumannValue[-stress, L/4 <= x <= 3 L/4 && y == h]},
    DirichletCondition[v[x, y] == 0, 0 <= x <= L && y == 0],
    DirichletCondition[u[x, y] == 0, x == 0 && y == 0]
    },
   {u, v},
   Element[{x, y}, mesh]
   ];

The same checks as above

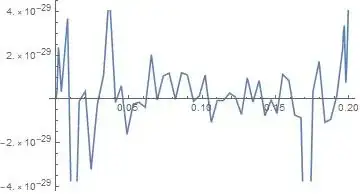
Plot[uif[x, 0], {x, 0, L}]

du = Head@D[uif[x, y], x];
Plot[du[x, 0], {x, 0, L}]
Plot[du[x, 0] - du[L - x, 0], {x, 0, L/2}]

No warning message and a symmetric result as expected.

Answer 1

There seems to be nothing wrong with the result given by NDSolve. The following FDM approach gives the same result. I've used pdetoae for the generation of difference equation:

L = 1;(*Length*)
h = 2/10;(*Height*)
Y = 20 10^10;(*Modulus of elasticity*)
ν = 33/100;(*Poission ratio*)
stress = 100 10^10;

lhsy = planeStress[Y, ν] /. Inactive[Div][a_, __] :> {0, 1}.a /. Inactive -> Identity;
lhsx = planeStress[Y, ν] /. Inactive[Div][a_, __] :> {1, 0}.a /. Inactive -> Identity;
bcxR = lhsx == 0 /. x -> L // Thread;
bcxL2 = lhsx == 0 /. x -> 0 // Thread(*//First*)// Last;
bcyL2 = lhsy == 0 /. y -> 0 // Thread // First;
bcyR = lhsy == {0, Piecewise[{{-stress, L/4 <= x <= (3 L)/4}}]} /. y -> h // Thread // 
   Simplify`PWToUnitStep;
{bcyL1, bcxL1} = With[{u = u[x, y], v = v[x, y]},
   {v == 0 /. y -> 0, u == 0 /. x -> 0}];
{domain@x, domain@y} = {{0, L}, {0, h}};
points = 50;
{grid@x, grid@y} = Array[# &, points, domain@#] & /@ {x, y};
difforder = 2;
(* Definition of pdetoae isn't included in this post,
   please find it in the link above. *)
ptoafunc = pdetoae[{u, v}[x, y], grid /@ {x, y}, difforder];
del = #[[2 ;; -2]] &;
ae = del /@ del@# & /@ 
   ptoafunc[planeStress[Y, ν] == 0 /. Inactive -> Identity // Thread];
aebc@x = del /@ ptoafunc[Flatten@{bcxL1, bcxL2, bcxR}];
aebc@y = ptoafunc[{bcyL1, bcyL2, bcyR} // Flatten];
varlst = Outer[#[#2, #3] &, {u, v}, grid@x, grid@y] // Flatten;
{b, m} = CoefficientArrays[Flatten@{ae, aebc /@ {x, y}}, varlst];
sollst = LinearSolve[m, -N@b];
{func@u, func@v} = 
  ListInterpolation[#, domain /@ {x, y}] & /@ ArrayReshape[sollst, {2, points, points}];
du = Head@D[func[u][x, y], x];
Plot[-du[x, 0], {x, 0, L}]
Plot[-du[x, 0] + du[L - x, 0], {x, 0, L/2}]

As mentioned in the comment above, it's not quite clear to me which Neumann b.c. should be chosen at $x=0$ and $y=0$, so I just found out the combination that produces the same result as FEM approach by trial and error. This is also the most… Er… good-looking result in my view. You can check other results yourself by modifying First to Last and Last to First in bcxL2 and bcyL2.

Answer 2

I believe both of your solutions are correct which we can show with additional plots. Your original solution clearly looks correct even though MMA gives you a warning. Let's look at you second soln. I have mostly used your code, but I added MaxCellMeasure->0.00001 to your mesh to smooth the plots and I changed your NDSolveValue function to:

sol = NDSolve[{planeStress[Y, \[Nu]] == {0, 
     NeumannValue[-stress, L/4 <= x <= (3 L)/4 && y == h]}, 
   DirichletCondition[v[x, y] == 0, 0 <= x <= L && y == 0], 
   DirichletCondition[u[x, y] == 0, x == 0]}, {u[x, y], 
   v[x, y]}, {x, y} \[Element] mesh];

u[x_, y_] = u[x, y] /. sol[[1]];
v[x_, y_] = v[x, y] /. sol[[1]];

This is your second (assymetric) solution and I match the plots you made, but let's go further. Check your DirichletCondition u=0 at x=0

Plot[u[0, y], {y, 0, h}]

That's close enough to 0. Now v=0 at y=0

Plot[v[x, 0], {x, 0, L}]

Also looks good. Now calculate the stresses so we can check.

eq1 = D[u[x, y], x] == (1/Y)*(sx - \[Nu]*sy);
eq2 = D[v[x, y], y] == (1/Y)*(sy - \[Nu]*sx);

sols = Solve[{eq1, eq2}, {sx, sy}] // Flatten // Simplify;

\[Sigma]x[x_, y_] = sx /. sols;
\[Sigma]y[x_, y_] = sy /. sols;

Look at the vertical stress at y=h where you have specified the stress.

Plot[\[Sigma]y[x, h], {x, 0, L}, PlotRange -> All]

Which I believe matches the vertical stress at the top you want and even appears to be symmetric. Check the stress value at the middle.

\[Sigma]y[L/2, h]
(*-99.9982*)

You will get closer to the value of 100 with a finer mesh. While I am no theoretical mathematician, one thing I have always learned is that a solution that satisfies the differential equation and also satisfies the boundary conditions is the correct solution and this assymetric solution does that, so evidently the constraint u=0 at x=0 while leaving the other end free causes an assymmetric solution that seems to be correct.

The solution that you are after, and the one that makes the most sense to me is to change your DirichletCondition to u=0 at x = L/2. When you do that, even though x = L/2 is not an edge, MMa solves it with no complaints about unspecified bc's and all your values become symmetric like your first solution, except that the plot of u is shifted.