How to display the smallest-circle enclosing random points

Question

Still a complete noob to Mathematica. How can I create random points on a x,y graph and then enclose all the points with the smallest possible circle?

score 7 · Answer 1 · answered Mar 28 '18 at 19:14

7

You can create random points with RandomReal:

pts = RandomReal[10, {100, 2}];

To find the minimal enclosing circle/disk, you can use BoundingRegion:

Graphics[{FaceForm[LightBlue], BoundingRegion[pts, "MinDisk"], Point[pts]}]

answered Mar 28 '18 at 19:14

Carl Woll

130,679
6
243
355

1

Does that contain both x and y values that would determine coordinates? – Stefan Rheeders Mar 28 '18 at 20:52

score 5 · Answer 2 · answered Mar 28 '18 at 21:56

SeedRandom[0];
pts = RandomReal[10, {100, 2}];

An alternate approach using NMinimize

reg = Disk[{x, y}, r];

Find the circular Disk with the smallest Area that contains all of the points

min = NMinimize[{Area[reg], (Element[#, reg] & /@ pts), r > 0}, {x, y, r}] // 
  Quiet

(* {132.395, {x -> 5.0594, y -> 5.21973, r -> 6.49173}} *)

area = min[[1]]

(* 132.395 *)

Comparing the area with Carl Woll's use of BoundingRegion

regCW = BoundingRegion[pts, "MinDisk"];

RegionCentroid[regCW]

(* {5.0594, 5.21973} *)

areaCW = Area[regCW]

(* 132.395 *)

(area - areaCW) // Chop[#, 10^-6] &

(* 0 *)

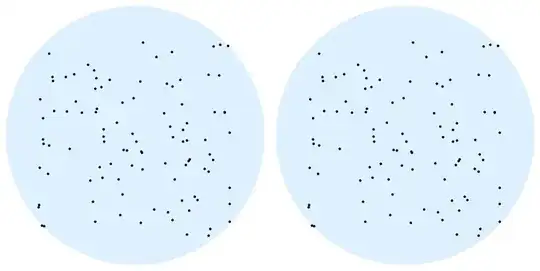
Row[{Graphics[{LightBlue, reg /. min[[2]], Black, Point[pts]}, 
   ImageSize -> 324],
  Graphics[{FaceForm[LightBlue], regCW, Point[pts]}, ImageSize -> 324]}]

HyperGroups · Answer 3 · 2020-01-08T11:10:26.600

0

You can use RandomPoint

pts=RandomPoint[Disk[],500];
Graphics[{PointSize[Tiny],Point[pts]}]

And RandomPoint support Region Objects.

pts=RandomPoint[Region, 500];
Graphics[{PointSize[Tiny],Point[pts]}]

So you can generate random points on a Region which could be a circle and then enclose all the points with the smallest possible Region which could be a circle?

Of course, you can bounding Region these points further like other answers done.

From 10.2 to later versions

edited Jan 08 '20 at 11:10

answered Jan 08 '20 at 10:34

HyperGroups

8,619
1
26
63

I think OP asked to find a disc containing some given points, not to generate random points in a given disc (though the question is pretty badly phrased). – Szabolcs Jan 08 '20 at 10:52
@Szabolcs He says: How can I create random points on...? – HyperGroups Jan 08 '20 at 11:04
Followed by "... on a x,y graph" (whatever that may be), not by "on a disc". – Szabolcs Jan 08 '20 at 11:07
1

@Szabolcs Yes, but RandomPoint support any Region, I just think this function is useful, so I add one Code. – HyperGroups Jan 08 '20 at 11:09

How to display the smallest-circle enclosing random points

3 Answers3