0
pp=ImplicitRegion[Sum[EuclideanDistance[{x,y},pt],{pt,CirclePoints[{0,0.75},
{5,0Degree},4]}]==24 &&(-1+0.04 x^2+0.8 y^2)^3==0.00032 x^2 y^3,{x,y}]
Reduce[Element[{x,y},pp],{x,y}]//LogicalExpand

I use above method to find the intersection point value,but 2 hours past, there's no any result.
Then I plot: 

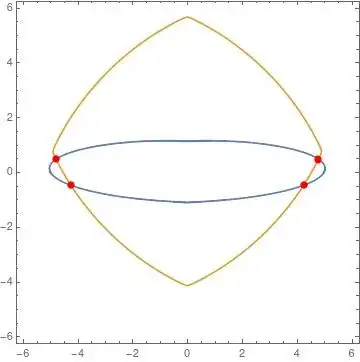
a=ContourPlot[(-1+0.04 x^2+0.8 y^2)^3==0.00032 x^2 y^3,{x,-6,6},{y,-6,6}];
b=ContourPlot[Sum[EuclideanDistance[{x,y},pt],{pt,CirclePoints[{0,0.75},
{5,0Degree},4]}]==24,{x,-6,6},{y,-6,6}];
Show[a,b]

It's easy to find there are intersection points.
plot How to calculate the intersection points value?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
kittygirl
  • 707
  • 4
  • 9
  • You have two problems here: your use of inexact numbers like 0.04 and 0.8, and your use of EuclideanDistance[], which introduces an Abs[] that gives solvers trouble. – J. M.'s missing motivation Mar 29 '18 at 17:22
  • Also, after looking into it, it seems the solutions involve the root of a degree-30 polynomial with terribly large coefficients. Do you really need an exact solution? – J. M.'s missing motivation Mar 29 '18 at 17:28
  • I really need exact solution! Within 2 hours, system didn't give me any solvers trouble notice. – kittygirl Mar 29 '18 at 17:28
  • 1
    But it's been running for two hours, as you say. Again, consider that your asking for the exact solution might be unreasonable, when an approximate one is adequate. – J. M.'s missing motivation Mar 29 '18 at 17:32
  • What's your approximate result?I don't understand why this calculation need long time but I am happy to ask a hard question. – kittygirl Mar 29 '18 at 17:40
  • I would say that it's need to solve a degree-30 polynomial with large coefficients contributes to the long evaluation time. Maybe look at this picture. – J. M.'s missing motivation Mar 29 '18 at 17:50
  • You mean my method is correct? Just need more time for CPU calculation? – kittygirl Mar 29 '18 at 17:54
  • My point was more that your desire for an exact solution is impractical. See this picture too, and note the exponent of the polynomial involved. – J. M.'s missing motivation Mar 29 '18 at 17:59
  • 1
    Just to make it clear: exact means a closed-form expression. Approximate solution means floats, like 0.123456. So if you want numerical values, then your problem can be easily solved. But if you actually want something exact, then you need to solve for the roots of a high-degree polynomial which takes a very long time (and might not even be possible). – anderstood Mar 29 '18 at 18:05
  • @anderstood,floats is ok for me,just like 0.3333 is ok even not 1/3. – kittygirl Mar 29 '18 at 18:13
  • OK so you should probably edit your question (replace exact with accurate for example). There are many answers on this site (see e.g. 42304). – anderstood Mar 29 '18 at 18:32

3 Answers3

4

Here is a graphic method: plot the intersection points in ContourPlot, extract them, then merge close points:

f1[x_, y_] = (-1 + 0.04 x^2 + 0.8 y^2)^3 - 0.00032 x^2 y^3;
f2[x_, y_] = 
  Sum[EuclideanDistance[{x, y}, pt], {pt, 
     CirclePoints[{0, 0.75}, {5, 0 Degree}, 4]}] - 24.;
plot = ContourPlot[{f1[x, y], f2[x, y]}, {x, -6, 6}, {y, -6, 6}, 
  Contours -> {{0}}, MeshFunctions -> {f1[#, #2] - f2[#, #2] &}, 
  Mesh -> {{{0, Directive[Red, PointSize[Large]]}}}, PlotPoints -> 400]
pts = plot[[1, 1]][[First@
     Cases[plot, Point[data_] :> data, Infinity]]];
Union[pts, SameTest -> (Norm[#1 - #2] < 0.1 &)]
(* {{-4.78877, 0.46492}, {-4.2477, -0.488119}, {4.24704, -0.488501}, 
{4.78815, 0.463675}} *)

enter image description here

If you want a greater accuracy, use these points are initial conditions for FindRoot:

Table[FindRoot[{f1[x, y], f2[x, y]}, Transpose[{{x, y}, p}]], {p, pts}]
 (* {{-4.78887, 0.465097}, {-4.24761, -0.488263}, {4.24761, -0.488263}, 
  {4.78887, 0.465097}} *)
anderstood
  • 14,301
  • 2
  • 29
  • 80
3

It seems to work okay with exact coefficients, over the Reals:

eqns = Sum[EuclideanDistance[{x, y}, pt], {pt, 
       CirclePoints[{0, 0.75} // Rationalize, {5, 0 Degree}, 4]}] == 
     24 && (-1 + 0.04 x^2 + 0.8 y^2)^3 == 0.00032 x^2 y^3 // 
   Rationalize;
pp = ImplicitRegion[eqns, {x, y}]
(*
ImplicitRegion[
 Sqrt[Abs[x]^2 + Abs[-(23/4) + y]^2] +
  Sqrt[Abs[-5 + x]^2 + Abs[-(3/4) + y]^2] +
  Sqrt[Abs[5 + x]^2 + Abs[-(3/4) + y]^2] +
  Sqrt[Abs[x]^2 + Abs[17/4 + y]^2] == 24 &&
   (-1 + x^2/25 + (4 y^2)/5)^3 == (x^2 y^3)/3125, {x, y}]
*)

sols = Solve[Element[{x, y}, pp], {x, y}, Reals]; // AbsoluteTiming
(*  {2.03908, Null}  *)

An approximation to sols:

{x, y} /. N@sols
(*{{-4.24761,-0.488263}, {4.24761,-0.488263}, {-4.78887,0.465097}, {4.78887,0.465097}}*)

Alternate exact solution:

gb = GroebnerBasis[Simplify[eqns, {x, y} ∈ Reals] /. Equal -> Subtract, {y, x}];

exact = Table[
   Root[Function /@ (Take[gb, j] /. {x -> #1, y -> #2}), Take[{i, 1}, j]],
   {i, 4}, {j, 2}];
exact // N
(*{{-4.78887,0.465097}, {-4.24761,-0.488263}, {4.24761,-0.488263}, {4.78887,0.465097}}*)
Michael E2
  • 235,386
  • 17
  • 334
  • 747
0

I read this thread ,I don't think I get a general method to find exact intersection.I post the script as below: 

FindCrossings2D[{f_, g_}, {x_, xmin_, xmax_}, {y_, ymin_, 
ymax_}] := {x, 
y} /. (FindRoot[{f[x, y] == 0, 
   g[x, y] == 
    0}, {{x, #[[1]]}, {y, #[[2]]}}] & /@ (ContourPlot[{f[x, y] == 
     0, g[x, y] == 0}, {x, xmin, xmax}, {y, ymin, ymax}][[1, 1]]))
f[x_, y_] := (-1 + 0.04 x^2 + 0.8 y^2)^3 - 0.00032 x^2 y^3;
g[x_, y_] := 
Sum[EuclideanDistance[{x, y}, pt], {pt, 
 CirclePoints[{0, 0.75}, {5, 0 Degree}, 4]}] - 24;
pts = FindCrossings2D[{f, g}, {x, -6, 6}, {y, -6, 6}]

ContourPlot[{f[x, y] == 0, g[x, y] == 0}, {x, -6, 6}, {y, -6, 6}, 
Epilog -> {AbsolutePointSize[6], Red, Point /@ pts}]
kittygirl
  • 707
  • 4
  • 9