Using Random walk on a region

Question

I want to simulate a random walk on two dimension equation using module. Checked the input so the path works

Walk[r_] := Module[{position, x, y, path},
position = {0, 0};
x = position[[1]];
y = position[[2]];
path = {position};
While[-r <= x <= r && -r <= y <= r,
x = x + RandomReal[{-1, 1}];
y = y + RandomReal[{-1, 1}];
position = {x, y};
AppendTo[path, position]
];
region = 
RegionPlot[-r <= s <= r && -r <= t <= r, {s, -r, r}, {t, -r, r}];
Show[region, ListPlot[path, Joined -> True, PlotStyle -> Red]]
]

Used Walk[] as a tester and it seems fine,

Walk[100]

but when I tried to use a given equation of the region, it does not display the region nor the path.

Walk[x^2 + y^2 <= 50 || -10 <= x <= 10 && 4 <= y <= 10, x, y, 1, 11]

Briefly, but the user wanted to simulate a path through a shape such as a circle or square, but I'm trying to simulate through an equation (that gives the region) such as the one I put above. — mastud89, Mar 30 '18 at 23:25
There's at least an issue with your r: in While[-r <= x <= r && -r <= y <= r, r should be values, but instead you use x^2 + y^2 <= 50 || -10 <= x <= 10 && 4 <= y <= 10, which does not make sense. — anderstood, Mar 30 '18 at 23:51
The answers in the link given by J.M. rely on a region, but you could easily convert your inequalities to a region (see ImplicitRegion for instance). — anderstood, Mar 30 '18 at 23:55

score 3 · Accepted Answer · answered Mar 31 '18 at 11:16

This is more of a comment on what is wrong with the code than an answer; the links in the comments point to-pretty much-authoritative implementations.

Looking at how Walk is implemented, it makes sense to evaluate something like Walk[100]-even though there are some minor tweaks in the code that will be proposed later in this note-but evaluating Walk[x^2 + y^2 <= 50 || -10 <= x <= 10 && 4 <= y <= 10, x, y, 1, 11] stops making sense from the first argument.

With the already provided implementation of Walk, argument 1 is expected to be a number whereas in the later evaluation it is an expression involving inequalities. Also, the initial implementation does not account for other arguments. Taking a guess, x,y are presumably the relevant variables in the expression involving inequalities; the rest of the input ie 1,11 is not to easy to understand. Without any explicit explanation, it is a matter or interpretation.

In what follows I will present a version of Walk that can accommodate inequalities:

(* requires a seed for reproducibility of random output *)
walk[r_, vars_?ListQ, seed_: 123456789] := Module[{reg, path, rands, rng},

  (* obtain the region *)
  reg = Reduce[r, vars, Reals];

  (* make reproducible *)
  BlockRandom[

   (* random steps in the unit ball *)
   rands := RandomReal[{-1, 1}, 2];

   path = NestWhileList[
    (* produce the *next* random point... *)
    # + rands &,
    (* begin from the origin... *)
    {0., 0.},
    (* while the *current* point is within the region... *)
    reg /. Thread[vars -> #] &

   ], RandomSeeding -> seed];

  (* correct for the last point outside the region *)
  path = Most@path;

  (* range for RegionPlot *)
  rng = Sequence @@ MapIndexed[
     {vars[[#2[[-1]]]], Sequence @@ #1} &,
     Through[{Min, Max}[#]] & /@ Transpose[path]
     ];

  (* output *)
  Show[
   {
    RegionPlot[reg, Evaluate@rng],

    ListPlot[path,
     PlotStyle -> {Red, PointSize[Small]}
     ]
    },

   PlotLabel -> Row[{"seed=", , seed}],

   Epilog -> {
     (* light blue point designates the starting point *)
     {Lighter@Blue, PointSize[Large], Point[First@path]},
     {Red, Opacity[0.4], Line[path]}
     }

   ]

  ]

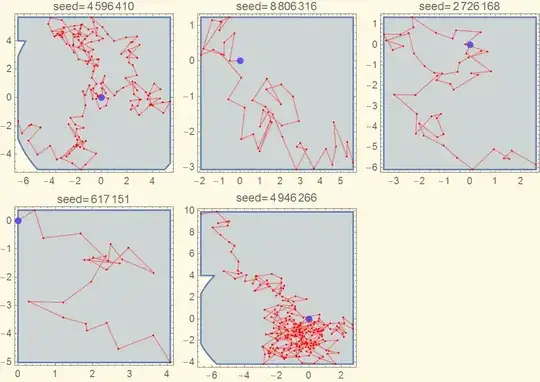
Evaluating

BlockRandom[
   walk[x^2 + y^2 <= 50 || -10 <= x <= 10 && 4 <= y <= 10, {x, y}, #] & /@ RandomInteger[{10^3, 10^7}, 5],
   RandomSeeding -> 321456987
 ] // Partition[#, 3, 3, {1, 1}, {}] & // Grid

produces

Following is the update of the original version of Walk:

(* again, use a seed for reproducibility *)
walk[r_, seed_: 123456789] := Module[{path},
  (* make reproducible *)
  BlockRandom[

   path = Most@NestWhile[
      (* produce next step *)
      # + RandomReal[{-1, 1}, 2]} &,
      (* start from the origin *)
      {0., 0.},
      (* check if current step is valid *)
      And @@ Thread[-r < #[[-1]] < r] &
      ], RandomSeeding -> seed
   ];

  (* assemble output *)
  Show[
   {
    RegionPlot[True, {s, -r, r}, {t, -r, r}],
    ListPlot[path, PlotStyle -> {Red, PointSize[Small]}]
    },
   PlotLabel -> Row[{"seed=", , seed}],
   Epilog -> {
     (* use a blue point to depict the origin *)
     {Lighter@Blue, PointSize[Large], Point[First@path]},
     {Red, Opacity[0.4], Line[path]}
     }
   ]
  ]

Evaluating

BlockRandom[
   walk[10, #] & /@ RandomInteger[{10^3, 10^7}, 5],
   RandomSeeding -> 456789123
   ] // Partition[#, 3, 3, {1, 1}, {}] & // Grid

produces

I think the 1 and 11 suppose to be was x and y equals to. Apparently the image is suppose to look something like this https://imgur.com/a/Ra23i — mastud89, Apr 01 '18 at 20:33
the linked image can be reproduced if you change in the first implementation of walk the range in RegionPlot appropriately, get rid of the line using Most, use RandomInteger instead of RandomReal, use Length on path to count the number of steps traversed and modify the Epilog in Show in a way to represent the highlighted points present in the linked image. Inputs 1 and 11 cannot correspond to the starting point of the walk. Having said that, it feels really awkward doing someone else's homework;please don't post your homework problems as questions — user42582, Apr 02 '18 at 08:18

Using Random walk on a region

1 Answers1