Series of piecewise functions

Question

Let $f_{0}(x):[0,1]\to[0,1]$ be defined by

$$f_{0}(x):=\begin{cases} 3x, & \text{if } x\in [0,\frac{1}{3}] \\ \\ -3x+2, & \text{if } x\in (\frac{1}{3}, \frac{2}{3}] \\ \\ 3x+2, & \text{if } x\in (\frac{2}{3},1] \end{cases} $$

Construct a sequence of function such that

$$f_{n+1}(x):=\begin{cases} \frac{1}{3}f_n(3x), & \text{if } x\in [0,\frac{1}{3}] \\ \\ \frac{1}{3}+\frac{1}{3}f_n(3x-1), & \text{if } x\in (\frac{1}{3}, \frac{2}{3}] \\ \\ \frac{2}{3}+\frac{1}{3}f_n(3x-2), & \text{if } x\in (\frac{2}{3},1] \end{cases},\;\; \forall n\in\mathbb{N}. $$

And then, take the series associated with this sequence.

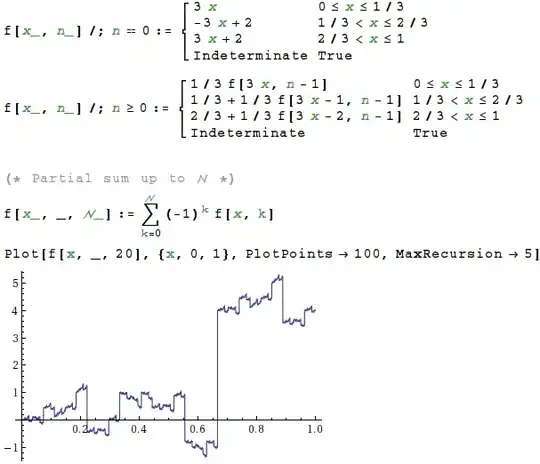
$$f(x):=\sum_{i=0}^{\infty}(-1)^{i}f_i(x).$$

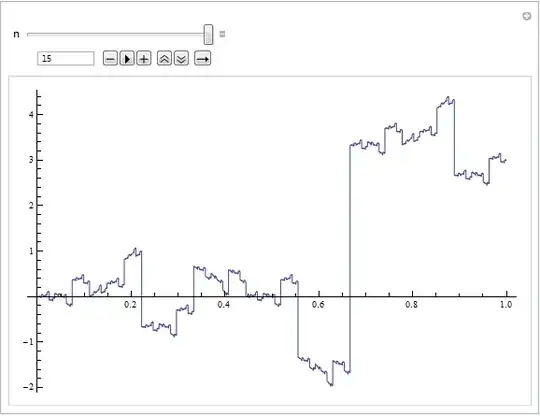
How do I plot some $f_n(x)$ (in function of n) and a good approximation for $f$? I want a plot of then separately and one in the same picture (with more than one $f_n$). Is it possible to make a "zoom" on the picture?

Furthermore, is it possible to create a simulation in which one gives a natural number $p$ as an input, and receives as output the graph of some $f_n$ (in function of n) and a good approximation for $f$?

$$f_{n}(x):=\begin{cases} \frac{1}{p}f_{n-1}(px), & \text{if } x\in [0,\frac{1}{p}] \\ \\ \frac{1}{p}+\frac{1}{p}f_{n-1}(px-1), & \text{if } x\in (\frac{1}{p}, \frac{2}{p}] \\ \\ .\\ .\\ .\\ \\ \frac{p-1}{p}+\frac{1}{p}f_{n-1}(px-p-1), & \text{if } x\in (\frac{p-1}{p},1] \end{cases} $$

Answer 1

You can pretty much enter your question in that form in Mathematica:

The first definition, f[x_, n_] /; n == 0, reads "define $f_n(x)$ in the case of $n=0$ to be the following". The fancy bracket is pretty frontend notation for the Piecewise function (shortcut: EscpwEsc). The next line is the same thing again, after that there's the definition of your function $f(x)$, which is the partial sum up to $\mathcal N$. I don't think you can use $\mathcal N=\infty$ in this case, as it will exceed the maximum recursion depth by, well, infinity. If you want to have an exact result, try using RSolve to get an explcit equation for $f_n(x)$.

If you want to evaluate the code above on your own, here's a copyable version:

f[x_, n_] /; n == 0 := Piecewise[{
    {3 x, 0 <= x <= 1/3},
    {-3 x + 2, 1/3 < x <= 2/3},
    {3 x + 2, 2/3 < x <= 1},
    {Indeterminate, True}
}]
f[x_, n_] /; n >= 0 := Piecewise[{
    {1/3 f[3 x, n - 1], 0 <= x <= 1/3},
    {1/3 + 1/3 f[3 x - 1, n - 1], 1/3 < x <= 2/3},
    {2/3 + 1/3 f[3 x - 2, n - 1], 2/3 < x <= 1},
    {Indeterminate, True}
}]
f[x_, _, \[ScriptCapitalN]_] := Sum[(-1)^k f[x, k], {k, 0, \[ScriptCapitalN]}]
Plot[f[x, _, 10], {x, 0, 1}, PlotPoints -> 100, MaxRecursion -> 5]

For the third part of your question, simply define $p$ as an additional parameter for your function, so it's something like f[x_, n_, p_] := ..., and edit the definitions accordingly.

Answer 2

You could define your functions this way :

f[0, x_] /; 0 <= x && x <= 1 := 
    Piecewise[{{3 x, x <= 1/3}, {-3 x + 2, 1/3 < x <= 2/3}, {3 x + 2, 2/3 < x}}]
f[n_, x_] /; 0 <= x && x <= 1 && n > 0 := 
    Piecewise[{{1/3 f[n - 1, 3 x], x <= 1/3}, 
               {1/3 + 1/3 f[n - 1, 3 x - 1], 1/3 < x <= 2/3},
               {2/3 + 1/3 f[n - 1, 3 x - 2], 2/3 < x}}]

and use Manipulate to plot functions for various n :

Manipulate[Plot[f[n, x], {x, 0, 1}], {n, 0, 15, 1}]

If you want to enlarge your plot, just click on it and drag a small orange square on the bottom right of the plot.

A straightforward way to approximate $f(x)$ is the following definition :

 F[n_, x_] := Sum[(-1)^k f[k, x], {k, 1, n}]

However that would be quite inefficient. Therefore we proceed along a different route.

F[0, x_] := f[0, x];
F[n_, x_] /; n > 0 := F[n, x] = F[n - 1, x] + (-1)^n f[n, x]

For a brief introduction to this technique read Functions That Remember Values They Have Found

In case you need a more precise plot you can use PlotPoints and MaxRecursion options in Plot, e.g.

Manipulate[Plot[F[n, x], {x, 0, 1}, PlotPoints -> 250], {n, 0, 15, 1}]