Although there exists this question with an answer I am not able to adopt it to my problem.
I have a 1d Langevin euqation which I solve with NDSolve.
How can I plot the derivative of the solution (see the plot below).
Here is my code:
m = 6.137*10^-13;
k = 1.5*m;
stddev = Sqrt[2*k]*Sqrt[m];
whiteNoise = WhiteNoiseProcess[stddev];
randomForce[t_Real] := RandomVariate[whiteNoise[t]];
SeedRandom[1];
s = NDSolve[
{m*x''[t] + k*x'[t] - randomForce[t] == 0, x[0] == 0, x'[0] == 0}
, x[t], {t, 0, 50}
, StartingStepSize -> 10^-3
, Method -> {"FixedStep", Method -> "ExplicitEuler"
}
, MaxSteps -> Infinity
];
Plot[x[t] /. s, {t, 0, 50}]
I want to plot x'[t] vs. t.
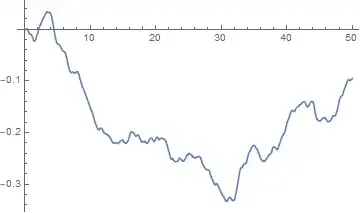

NDSolve:x[t]instead ofx. The I can write also:Plot[x'[t] /. s, {t, 0, 50}]– mrz Apr 06 '18 at 16:13