How to get accurate intersection point value of Parametric equation?

Question

I have parametric equation and normal equation,I don't know how to get accurate intersection point value of them.
I can only use a imprecise method as below:

a = ContourPlot[(-1 + x^2/5 + y^2/5)^3 == (x^2 y^2)/12, {x, -7, 7}, {y, -7, 7}];  
b = ParametricPlot[{1. (2.35 - 
   0.8603646545265691 Cos[t] Sin[t]^(1/4) + 1.2287280664334876 Sin[t]^(5/4)), 
1. (0. - 1.2287280664334876 Cos[t] Sin[t]^(1/4) - 0.8603646545265691 Sin[t]^(5/4))}, {t, 0, 2 Pi}]; 
pts = Graphics`Mesh`FindIntersections@Show[a, b]  
Show[a, b, Graphics[{RGBColor[0, 0.7, 0], PointSize -> 0.025, Point[pts]}]]

It's obvious that has no 4 intersection points. So, how to use a accurate method to get accurate intersection point value?

What are these parameters: 1.2287280664334876 and 0.8603646545265691. where do they come frome? You should know that providing exact values appears to be rewarding in Mathematica. — Artes, Apr 07 '18 at 13:26

Henrik Schumacher · Answer 1 · 2018-04-07T14:32:46.933

With the function

f = X \[Function] (-1 + X[[1]]^2/5 + X[[2]]^2/5)^3 - (X[[1]]^2 X[[2]]^2)/12;

and the curve

γ = t \[Function] {1. (2.35 - 0.8603646545265691 Cos[t] Sin[t]^(1/4) + 1.2287280664334876 Sin[t]^(5/4)), 
    1. (0. - 1.2287280664334876 Cos[t] Sin[t]^(1/4) - 0.8603646545265691 Sin[t]^(5/4))};

you are looking for roots of f[γ[t]]. NSolve can do that:

pts = γ[t] /. NSolve[{f[γ[t]] == 0, 0. <= t <= 2. Pi}, t];
a = ContourPlot[f[{x, y}] == 0, {x, -4, 4}, {y, -4, 4}, ContourStyle -> ColorData[97][2]];
b = ParametricPlot[γ[t], {t, 0, 2 Pi}];
Show[a, b, Graphics[{PointSize[0.02], ColorData[97][4], Point[pts]}]]

So there are four intersection, but they are quite different from what Graphics`Mesh`FindIntersections returns.

score 2 · Accepted Answer · answered Apr 07 '18 at 14:30

I share Artes's plea in the comments to mention how you obtained such magic constants like 1.2287280664334876 in your equations, as that might ease symbolic solutions. Nevertheless:

Method 1:

MeshFunctions, once more, is usable for this kind of problem:

ParametricPlot[{1. (2.35 - 0.8603646545265691 Cos[t] Sin[t]^(1/4) +
                1.2287280664334876 Sin[t]^(5/4)), 
                1. (0. - 1.2287280664334876 Cos[t] Sin[t]^(1/4) - 
                0.8603646545265691 Sin[t]^(5/4))}, {t, 0, 2 π},
               Mesh -> {{0}}, 
               MeshStyle -> Directive[RGBColor[0.7, 0, 0], AbsolutePointSize[5]], 
               MeshFunctions -> {Function[{x, y, t},
                                          (-1 + x^2/5 + y^2/5)^3 - (x^2 y^2)/12]}]

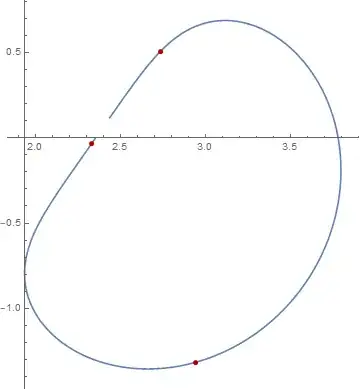
intersections

Cases[Normal[%], Point[pt_] :> pt, ∞]
   {{2.32563, -0.0349495}, {2.73159, 0.509025}, {2.94152, -1.31727}}

Method 2:

Use a Weierstrass substitution to help convert the parametric equation into an implicit Cartesian one:

tmp = Eliminate[MapAll[TrigExpand, Thread[{x, y} ==
                {(2.35 - 0.8603646545265691 Cos[t] Sin[t]^(1/4) + 
                  1.2287280664334876 Sin[t]^(5/4)),
                 (-1.2287280664334876 Cos[t] Sin[t]^(1/4) -
                  0.8603646545265691 Sin[t]^(5/4))} /. t -> 2 ArcTan[u]]], u];

(* alleviate sudden coefficient swell *)
tmp = Expand[Subtract @@ tmp];
tmp = Expand[tmp/Max[CoefficientList[tmp, {x, y}]]]

Now we can use NSolve[]:

{x, y} /. NSolve[{tmp == 0, (-1 + x^2/5 + y^2/5)^3 - (x^2 y^2)/12 == 0}, {x, y}, Reals]
   {{2.73164397095681, 0.509126233763010}, {2.42604085249915, 0.108583410750758},
    {2.42599009519994, 0.108539249717106}, {2.32555967012562, -0.0349062696627526},
    {2.32555782100012, -0.0349051879461614}, {2.94152191912221, -1.31727498432471}}

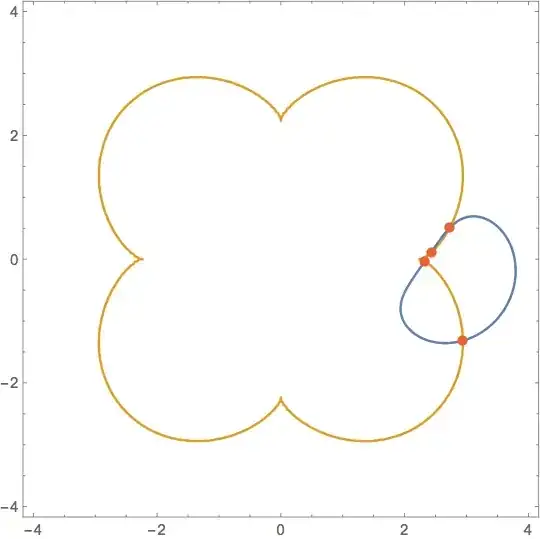
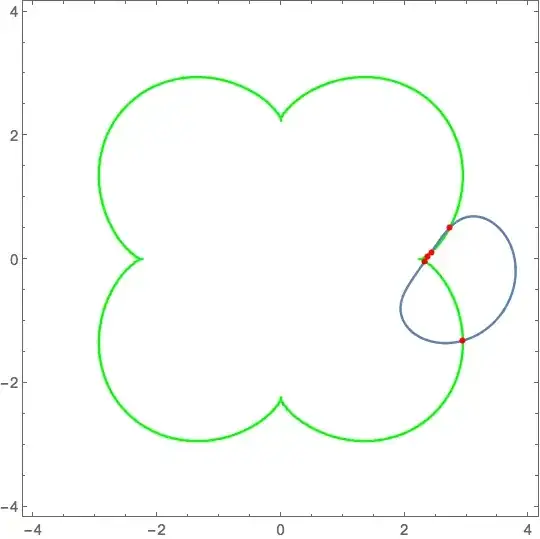
Show the intersection points:

Show[ContourPlot[(-1 + x^2/5 + y^2/5)^3 == (x^2 y^2)/12, {x, -4, 4}, {y, -4, 4}], 
    ParametricPlot[{1. (2.35 - 0.8603646545265691 Cos[t] Sin[t]^(1/4) + 
                    1.2287280664334876 Sin[t]^(5/4)), 
                    1. (0. - 1.2287280664334876 Cos[t] Sin[t]^(1/4) - 
                    0.8603646545265691 Sin[t]^(5/4))}, {t, 0, 2 π}], 
    Epilog -> {Directive[RGBColor[0, 0.7, 0], AbsolutePointSize[6]], Point[%]}]

two curves and their intersection points

There's little difference between method 1 and method 2.Which method should I trust more? — kittygirl, Apr 07 '18 at 15:21
Meet me halfway: I'll explain those if you tell us where those constants came from, just as Artes asked. — J. M.'s missing motivation, Apr 07 '18 at 19:54

score 0 · Answer 3 · answered Apr 07 '18 at 16:06

Clear[x, y, t]

eqns = {(-1 + x^2/5 + y^2/5)^3 == (x^2 y^2)/12,
    x == (2.35 - 0.8603646545265691 Cos[t] Sin[t]^(1/4) + 
       1.2287280664334876 Sin[t]^(5/4)), 
    y == (-1.2287280664334876 Cos[t] Sin[t]^(1/4) - 
       0.8603646545265691 Sin[t]^(5/4)), 
    0 <= t <= 2 Pi, -4 < x < 4, -4 < y < 4} // Rationalize[#, 0] &;

(pts = NSolve[eqns, {x, y, t}, WorkingPrecision -> 15]) // Column

This indicates that there are five points of intersection; however, the second one is an extraneous root.

And @@@ (eqns /. pts)

(* {True, False, True, True, True} *)

Show[
 ContourPlot[Evaluate@eqns[[1]], {x, -4, 4}, {y, -4, 4}, 
  ContourStyle -> Green],
 ParametricPlot[{eqns[[2, -1]], eqns[[3, -1]]}, {t, 0, 2 Pi}],
 Epilog -> {Red, AbsolutePointSize[4], 
   Tooltip[Point[{x, y}], {x, y, t}] /. # & /@ pts}]

To see that the second solution is not valid, you need to zoom in on the plot

Show[
 ContourPlot[Evaluate@eqns[[1]], {x, 2, 3}, {y, -1.5, .75}, 
  ContourStyle -> Green, PlotPoints -> 100],
 ParametricPlot[{eqns[[2, -1]], eqns[[3, -1]]}, {t, 0, 2 Pi}, 
  PlotPoints -> 100],
 Epilog -> {Red, AbsolutePointSize[4], 
   Tooltip[Point[{x, y}], {x, y, t}] /. # & /@ pts}]

How to get accurate intersection point value of Parametric equation?

3 Answers3

Method 1:

Method 2:

Linked