Recently I tried to check a result of integration which should be a linear combination of the Riemann $\zeta\;$-function at various arguments, the coefficients of the combination being of primary interest.
Unfortunately Mathematica have expanded all occurrences of $\zeta\;$-functions with even integer arguments.
Is there a way to prevent it from doing that?
A sample code:
Integrate[ Log[1-x]^5/x^5, {x, 0, 1}]
This is even simpler (thanks to @CarlWoll):
ClearSystemCache[];
Block[{Zeta = Inactive[Zeta]},
Integrate[Log[1 - x]^5/x^5, {x, 0, 1}]]
Original answer:
Using the Gayley-Villegas trick:
Internal`InheritedBlock[{Zeta},
Unprotect[Zeta];
Zeta[a_Integer /; a > 1] /; ! TrueQ[$in] := Block[{$in = True},
Inactive[Zeta][a]
];
Protect[Zeta];
Integrate[Log[1 - x]^5/x^5, {x, 0, 1}]
]
Note: The integral is actually computed in terms of limits of an expression involving PolyLog[n, 1-x] (for n = 2,3,4,5); we could do something similar for PolyLog as was done for Zeta above. However PolyLog actually evaluates to Zeta first, which is why the above works in this case. I mention it in case PolyLog does not evaluate to Zeta in a future version. And it's possible the integral will not be computed in terms of PolyLog in the future, too, I suppose. In any case, I thought some explanation of why the code happens to work in this case would be helpful. (It will certainly help me a year from now when someone asks why this doesn't work, and I won't remember a thing about it.)
Mathematica is a term rewriting system and there are various ways to suppress automatic evaluation of expressions. The system doesn't evaluate Zeta for odd integer arguments (see e.g. Zeta[Range[2, 20]]). Zeta[n] yields expressions involving n-th powers of Pi, thus one of possible ways to achieve the goal would be e.g.
Integrate[Log[1 - x]^5/x^5, {x, 0, 1}] /.
Times[x_, Pi^n_Integer] :> x Pi^n Inactivate[Zeta[n]]/Zeta[n] //
TraditionalForm
Another way is to use HoldForm[Zeta[n]] instead of Inactivate[Zeta[n]] however the latter is more universal and handy. You can use Activate (also with appropriate patterns) to evaluate the expression, e.g.
Activate[%]
-((5 Pi^2)/6) - (11 Pi^4)/18 - 30 (Zeta[3] + Zeta[5])
Nevertheless using such a replacement should be appropriately restricted to avoid possible ambiguities with expressions involving symbolic results in terms of powers of Pi.
Times[x_, π^n_?EvenQ]
– J. M.'s missing motivation
Apr 13 '18 at 18:11
Integrate[BesselK[0, x]^2, {x, 0, Infinity}] are subject to transform or not.
– Artes
Apr 13 '18 at 18:23
Inactivate which could be exploited. With an example at hand this could be worked out, nonetheless there is no obvious general way.
– Artes
Apr 13 '18 at 20:21
Range[1,20]Sin[Pi/Range[1,20]]. It is really hard to find a method of "postprocessing". It would be better somehow tell Mathematica never evaluate Sin. But as I understood it is impossible.
– drer
Apr 13 '18 at 22:23
Zeta is evaluating that we have powers of π in the answer. Executing Block[{Zeta = Inactive[Zeta]}, Integrate[Log[1 - x]^5/x^5, {x, 0, 1}]] suggests that the powers of π are computed without using Zeta. If so, one cannot blame the evaluation of special functions for returning a correct answer in a certain form.
– Michael E2
Apr 14 '18 at 01:41
-5 (Zeta[2]+6Zeta[3]+11Zeta[4]+6Zeta[5]) as it was desired. Thank you!!!
– drer
Apr 14 '18 at 07:41
Zeta. I have really no clue what is happening here.
– drer
Apr 14 '18 at 08:31
Integrate[Log[1 - x]^n/x^n, {x, 0, 1}]] with some n either inside or outside of the Block[{Zeta=Inactive[Zeta]},...], all subsequent calls with the same n result in the same output as in the first one, completely independent from the art of the call (inside or outside of the Block). It however does not influence subsequent calls of the command with a different not yet used n.
– drer
Apr 14 '18 at 09:30
Limit of an expression in terms of PolyLog, Log and powers of x, not in terms of Zeta. It's the polylogs that evaluate to zeta inside the limit call. Another possible issue is that replacement rules can be used to rewrite expressions, not just evaluation. -- As for reproducibility, note that sometimes expressions are cached and reused, rather than recalculated. ClearSystemCache can sometimes be used to reset the cache.
– Michael E2
Apr 14 '18 at 13:12
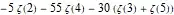
ClearSystemCache[]; Block[{Zeta = Inactive[Zeta]}, Integrate[Log[1 - x]^5/x^5, {x, 0, 1}]]. I tried using thisBlockearlier and it didn't work. When I saw your answer, I realized that the cache was interfering. – Carl Woll Apr 14 '18 at 15:50Integrate, even worse if we inactivatePolyLogin the same way. Makes me wonder how safe it is. In fact, I got a wrong answer with one thing I tried (not shown). On the other hand, pattern matching can be made much harder if there are coefficients in the integrand that obfuscate or destroy the pattern. But done your way, it is perfectly safe. (+1 to your answer a while ago.) – Michael E2 Apr 14 '18 at 17:49