How do I get my simulation to run?

Question

I am simulating a birth-death population process. My code is

RESULTS = {};
For[iterator = 1, iterator < 21, iterator++,
 n = 25; t = 0;
 results = {{t, n}};
 mu = 1; lam = 1;
 While[t < 200,
  death = lam*n;
  birth = mu*n;
  rate = death + birth;
  deltaT[r_] := -1/r*Log[RandomReal[]];
  t1 = deltaT[rate];
  t = t + t1;
  rand = RandomReal[]*rate;
  Which[
   rand <= death, n = n - 1,
   True, n = n + 1
   ];
  results = Append[results, {t, n}];
  ];
 AppendTo[RESULTS, results];
 ]

I am getting an error message that says 'Infinite expression 1/0 encountered. >>'.

I'm not quite sure why this is. I think it might be because the population dies out so the rate would be zero, hence deltaT[r_] would be trying to work out -1/0.

Is this correct?

How do I get around this?

I understand that's the reason why. I therefore want the simulation to run up until the point to which the rate becomes 0, then stop. How do I adapt my code so that it does this? @HenrikSchumacher — Mlo27, Apr 14 '18 at 15:49
@Mlo27 For rate to be zero, you have to have n = 0, right? So you need to change your Which statement so that n does not become zero. — C. E., Apr 14 '18 at 15:50
You could put a If[Abs[rate]<100. $MachineEpsilon,Break[]] before the point of division. — Henrik Schumacher, Apr 14 '18 at 16:01
Have you seen this? https://mathematica.stackexchange.com/questions/158212/simple-birth-death-process — OkkesDulgerci, Apr 14 '18 at 17:32
@OkkesDulgerci I have. I don’t want to change code massively though. I just want to add a command so that the simulation stops when I get the error. — Mlo27, Apr 14 '18 at 17:49

score 2 · Answer 1 · answered Apr 14 '18 at 18:02

As @Henrik mentioned in comment, you can break simulation if rate<0.

RESULTS = {};
For[iterator = 1, iterator < 21, iterator++, n = 25; t = 0;
 results = {{t, n}};
 mu = 1; lam = 1;
 While[t < 200, death = lam*n;
  birth = mu*n;
  rate = death + birth;
  If[Abs[rate] < 100. $MachineEpsilon, Break[]];
  deltaT[r_] := -1/r*Log[RandomReal[]];
  t1 = deltaT[rate];
  t = t + t1;
  rand = RandomReal[]*rate;
  Which[rand <= death, n = n - 1, True, n = n + 1];
  results = Append[results, {t, n}];];
 AppendTo[RESULTS, results];]

ListLinePlot[RESULTS, InterpolationOrder -> 0]

user42582 · Answer 2 · 2018-04-15T09:50:26.827

I have tried to make a functional version of the original code that incorporates the observation made in the comments by multiple discussants that n=0 breaks the original code.

This implementation uses NestWhileList to substitute for the innermost While and NestList replaces the outermost For.

Block[{test, compose},

  With[{no = 25, to = 0, te = 200, mu = 1, lam = 1, iterator = 20, seedo = 123456987},

    (* input {t, n, r}; returns 'True' is t < te (=200) and r \[NotEqual] 0 *)
    test = #1 < te && #3 != 0 &;

    (* input {t, n}; returns {t, n, r} *)
    compose = {##, (lam + mu) #2} &;

    (* get rid of the first entry in the output (= NestList's second argument (check documentation) *)
    data = Rest@NestList[

      (* create the seed to be used in BlockRandom (used for reproducibility) *)
      With[{seed = #[[1]] + 1},

        (* output = {{seed, {{t, n, r},.. }}.. } *)
        {seed, BlockRandom[

          NestWhileList[

            With[{t = #[[1]], n = #[[2]], r = #[[-1]], rands = RandomReal[{0, 1}, 2]},

              (* perhaps redundant With - helps readability *)
              With[{death = lam n},

               (* produce next {t, n, r} from {t, n} *)
               Apply[compose][{
                 t - 1/r Log[rands[[1]]],
                 Which[
                   r rands[[-1]] <= death, n - 1,
                   True, n + 1
                  ]
                }]

               ]
             ] &,

            (* init = {t, n, r} *)
            Apply[compose][{to, no}],

            (* check if t < 200 and r\[NotEqual]0 *)
            Apply[test][#] &], RandomSeeding -> #[[1]]]}

     (* init NestList *)
     ] &, {seedo, {}}, iterator];

  ]

 ]

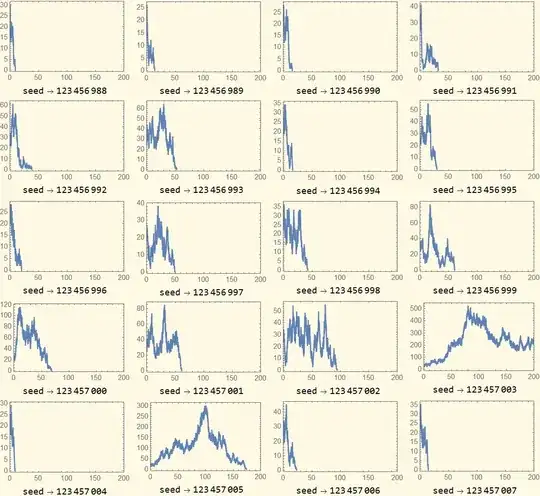
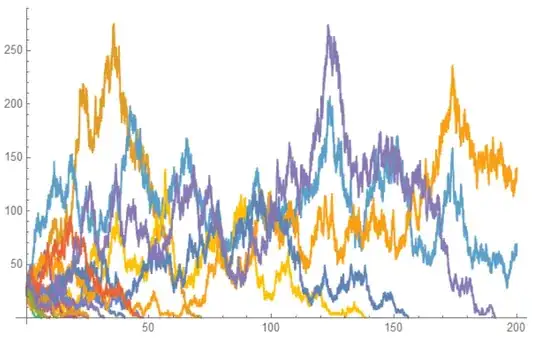
The plots were produced with:

ListLinePlot[
  Part[#, -1, All, {1, 2}],
  Frame -> True,
  PlotLegends -> Placed[Row[{HoldForm[seed] -> Part[#, 1]}], Bottom],
  InterpolationOrder -> 0,
  PlotRange -> {{0, 200}, Automatic}
 ] & /@ data // Partition[#, 4, 4, {1, 1}, {}] & // Grid

How do I get my simulation to run?

2 Answers2