2

Let's say I have a system of linear differential equations, e.g.: \begin{align*} x'(t) &= -\frac{1}{10}x(t) - y(t) \\ y'(t) &= x(t) \end{align*}

Is there a way for me to have Mathematica "solve" it for $x(t)$ by eliminating other variables to obtain the following? \begin{align*} x(t) = -\frac{1}{10} x'(t) - x''(t) \end{align*}

The naive attempt of

Reduce[{x'[t] == -x[t]/10 - y[t], y'[t] == x[t]}, x[t]]

gives

y[t] == -x'[t] - y'[t]/10 && x[t] == y'[t]

which is unhelpful...

user541686
  • 1,317
  • 7
  • 18
  • 2
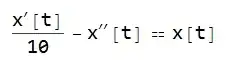
    Eliminate[{D[x'[t] + 1/10 x[t] + y[t], t] == 0, y'[t] - x[t] == 0}, y'[t]]. One can solve the system directly with DSolve, nevertheless it seems you're asking with this special case about a more general problem: differential elimination, see Working with a system of differential equations that cannot be solved explicitly. – Artes Apr 18 '18 at 09:38
  • @Artes: Yeah, exactly, that's what I'm trying to do. DSolve doesn't help since I don't want an explicit solution here. Using Eliminate seems to partially get there but not quite, because then I'm not sure which rows I should differentiate, and it seems to choke when I differentiate everything (With[{sys = {x'[t] == -x[t]/10 - y[t], y'[t] == x[t]}}, Eliminate[Join[sys, D[sys, t]], {y'[t], y[t]}]]). The link seems interesting... am I correct in interpreting it that there are no packages for this? – user541686 Apr 18 '18 at 10:06
  • 1
    You will never know in advance the proper or the best method of solving problems. You need no package, by a simple inspection (or just by trial and error method) you should figure out which functions you should differentiate, otherwise there will be no hints from any "sophisticated packages" to achieve the goal. – Artes Apr 18 '18 at 10:27
  • @Artes: I mean it's a little hard to do figure out which functions to differentiate "by a simple inspection" when I'm not standing next to the shoulder of the person trying to use my function... or when I'm trying to do this myself with 20 different systems that aren't already in a convenient format... otherwise we'd never keep most computer programs around; we'd just figure out everything by inspection and hard-code the final answer. – user541686 Apr 18 '18 at 10:35
  • This Wolfram Community thread has a response indicating how to do this in cases where prolongation (taking more derivatives) might be required. – Daniel Lichtblau Apr 18 '18 at 13:51
  • @DanielLichtblau: Thank you!!! That helped me figure out it out!! I guess Eliminate works after all; you just have to use it correctly! – user541686 Apr 18 '18 at 19:48

3 Answers3

4

Try this:

x'[t] == -x[t]/10 - y[t] /. x -> (y'[#] &)

enter image description here

Another way around:

y'[t] == x[t] /. y -> (-x'[#] + x[#]/10 &)

yielding

enter image description here

Done. Have fun!

Alexei Boulbitch
  • 39,397
  • 2
  • 47
  • 96
  • Uhm, thanks, but don't you think this is a little... too specific to the problem? I obviously didn't need to solve that exact example when I already know the answer to it... and if I already had everything in a nice-to-substitute-by-hand form then I would just substitute it by hand. I'm trying to do it in general for linear ODEs where doing so is possible for the computer. – user541686 Apr 18 '18 at 09:57
  • 1
    @Mehrdad There is no universal trick to do that. On the other hand, if you need something more complex, post it. I answered just what you asked. – Alexei Boulbitch Apr 18 '18 at 19:32
  • That's literally what I already did... the title said "how to eliminate variables in ODE" (not "in this very particular ODE") and the body said "say I have a system of linear differential differential equations, e.g. [this one]" (not "say I have this very particular ODE")... – user541686 Apr 18 '18 at 19:33
  • 2
    @Mehrdad, please be fair in your comments. If you do not post a "more general/complicated" example (not a simple/easy one), it will be difficult to answer a helpful solution. In this case, I think that the solution proposed is quite easy to generalise for being appropriate to a more complex system of ODEs. – José Antonio Díaz Navas Apr 19 '18 at 17:02
  • @JoséAntonioDíazNavas: I thought it was a very fair comment? I made it extremely clear in the question that I was merely giving an example of a linear ODE; I'm not sure where the ambiguity was. Those who commented under the question clearly understood the problem. If people decide to ignore everything I said and just solve the examples then they can do the same regardless of what the actual examples are... – user541686 Apr 19 '18 at 20:19
2

I found something that works, thanks to the help of those who commented on the question.

Input:

With[{f = Function[t,
    {x'[t] + x[t]/10 + y[t],
     x[t] - y'[t] + z[t],
     x[t] + 3 y[t] - z'[t]}]},
 With[{ndiff = Function[{exp, t}, Array[D[exp, {t, #}] &, Length[f[t]] + 1, 0]]},
  Eliminate[
   Join @@ ndiff[f[t], t] == 0,
   Complement[
    ndiff[f[t], t] // Variables,
    ndiff[x[t], t]]]]]

Output:

-10 x'''(t) - x''(t) + 20 x'(t) == 7 x(t)
user541686
  • 1,317
  • 7
  • 18
1

Use the second equation as a rule.

ode = x'[t] == -1/10 x[t] - y[t];

yprule = y'[t] -> x[t];

Take the derivative of ode wrt t

D[ode[[1]], t] == D[ode[[2]], t] /. yprule

(* x''[t] == -(1/10) x'[t] - x[t] *)

Another way

D[ode[[1]], t] == D[ode[[2]], t] /. y -> (Integrate[x[#1], #1] & )

Same answer

Bill Watts
  • 8,217
  • 1
  • 11
  • 28