Plot a derivate function and the tangent to a plot

Question

Being f(x)= f(x) = - x^2 + 4x - 3 if x < 3 f(x) = 3 - x | x - 4 | if x >= 3 and with h (x) = (x - 4) f(x). I have to prove that the derivate of h exists in x = 4. Then plot the function h and the tangent to the plot in x=4 in the same plot.

Answer 1

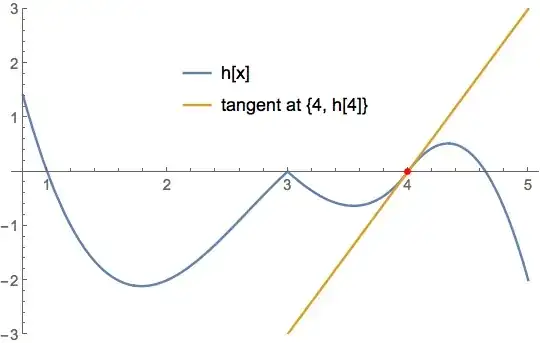
f[x_] = Piecewise[{{-x^2 + 4 x - 3, x < 3}}, 3 - x*Abs[x - 4]];

h[x_] = (x - 4) f[x];

At x == 4 the derivative of h[x] exists in the limit

Limit[h'[x], x -> 4]

(* 3 *)

So the equation of the tangent passing through {4, h[4]} is 3 (x - 4) + h[4]

Plot[{h[x], 3 (x - 4) + h[4]}, {x, 0.8, 5},
 PlotRange -> {-3, 3},
 Epilog -> {Red, PointSize[Medium], Point[{4, h[4]}]},
 PlotLegends -> Placed[{"h[x]", "tangent at {4, h[4]}"}, {.5, .75}]]