Better way to calculate angle between lines?

Question

I wrote anglecalc to calculate the clockwise angle from line a to b. Initially I thought VectorAngle would do it, but I had to add extra functionality. Is there a simpler way?

rotationangle[{i_, j_}] := Which[
  i >= 0 && j >= 0, VectorAngle[{1, 0}, {i, j}],
  i < 0 && j >= 0, VectorAngle[{0, 1}, {i, j}] + Pi/2,
  i < 0 && j < 0, VectorAngle[{-1, 0}, {i, j}] + Pi,
  i >= 0 && j < 0, VectorAngle[{0, -1}, {i, j}] + 3 Pi/2]

quadrant[{i_, j_}] := Which[
  i >= 0 && j >= 0, 1, i < 0 && j >= 0, 2,
  i < 0 && j < 0, 3, i >= 0 && j < 0, 4]

anglecalc[u_, v_] := Module[{a, theta, r},
  a = VectorAngle[u, v];
  theta = -rotationangle[u];
  r = RotationTransform[theta];
  If[quadrant[r[v]] > 2, 2 Pi - a, a]]

Test cases

r = RotationTransform[90 Degree];

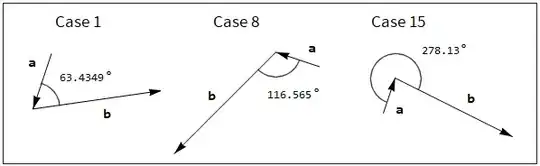
(* case 1 *)
{a, b} = {{{4, 3}, {3, 0}}, {{3, 0}, {10, 1}}};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 2 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.22], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 3 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 4 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.22], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 5 *)
{a, b} = {{{4, 3}, {3, 0}}, {{3, 0}, {10, -7}}};
Graphics[{Arrowheads[0.12], Arrow[{a, b}]}, ImageSize -> {120, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 6 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.09], Arrow[{a, b}]}, ImageSize -> {Automatic, 120}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 7 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.12], Arrow[{a, b}]}, ImageSize -> {120, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 8 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.09], Arrow[{a, b}]}, ImageSize -> {Automatic, 120}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 9 *)
{a, b} = {{{4, 3}, {3, 0}}, {{3, 0}, {-7, -5}}};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 10 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.13], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 11 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 12 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.13], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 13 *)
{a, b} = {{{4, 3}, {3, 0}}, {{3, 0}, {-7, 5}}};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 14 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.21], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 15 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.1], Arrow[{a, b}]}, ImageSize -> {150, Automatic}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

(* case 16 *)
{a, b} = r /@ {a, b};
Graphics[{Arrowheads[0.21], Arrow[{a, b}]}, ImageSize -> {Automatic, 150}]
{u, v} = a - b;
N[anglecalc[v, -u] 180/Pi]

First thought occurs to me is to use dot and cross product of 3D vectors. — Αλέξανδρος Ζεγγ, Apr 26 '18 at 11:12
You want to find the angle by which a is to be turned clockwise in order to point in the opposite direction of b? — LLlAMnYP, Apr 26 '18 at 12:31
@LLlAMnYP My code developed a bit accidentally. The arrows are just to show the Line order, not the vectors. I reversed the direction of one vector in the function call, e.g. anglecalc[v, -u]. — Chris Degnen, Apr 26 '18 at 13:07
Might I ask if you're looking for something particularly special in an answer (since you haven't accepted one yet)? — LLlAMnYP, May 02 '18 at 11:28
@LLlAMnYP Heh, yes I've found it difficult to choose between your answer and chyanog's because the latter actually shows how VectorAngle can be applied. — Chris Degnen, May 02 '18 at 11:37

score 24 · Accepted Answer · answered Apr 26 '18 at 12:43

24

This passed all test cases, I think:

anglecalc[vec1_, vec2_] := Mod[(ArcTan @@ vec2) - (ArcTan @@ vec1), 2 π]

answered Apr 26 '18 at 12:43

LLlAMnYP

11,486
26
65

3

Some amazing answers here. – Chris Degnen Apr 26 '18 at 12:54

Henrik Schumacher · Answer 2 · 2018-04-26T12:12:34.437

For a start, you can use this signed-angle function, which involves the two-argument version of ArcTan:

myVectorAngle[{x1_, x2_}, {y1_, y2_}] := Evaluate[
  With[{code = ReIm[(y1 + I y2)/(x1 + I x2)] // ComplexExpand // Simplify},
   ArcTan @@ code]
  ]

Some usage example:

{a, b} = {{{4, 3}, {3, 0}}, {{3, 0}, {10, 1}}} // N;
Pi - myVectorAngle @@ (a - b)

1.10715

If you have to use that a lot, you may switch to the following compiled function:

cf = Block[{P, PP},
   PP = Table[Compile`GetElement[P, i, j, k], {i, 1, 2}, {j, 1, 2}, {k, 1, 2}];
   With[{code = 
      N[Pi] - myVectorAngle[PP[[1, 1]] - PP[[1, 2]], PP[[2, 1]] - PP[[2, 2]]]},
    Compile[{{P, _Real, 3}},
     code,
     CompilationTarget -> "C",
     RuntimeAttributes -> {Listable},
     Parallelization -> True,
     RuntimeOptions -> "Speed"
     ]
    ]
   ];

cf[{a, b}]

1.10715

score 10 · Answer 3 · answered Apr 26 '18 at 11:22

10

kek[x_] := 2 \[Pi] - If[x > 0, x, 2 \[Pi] + x]
anglecalc2[u_, v_] := kek[(ToPolarCoordinates[RotationMatrix[{v, {1, 0}}].(u)][[2]])]

answered Apr 26 '18 at 11:22

Vsevolod A.

959
5
15

chyanog · Answer 4 · 2020-12-02T10:40:37.197

Clear["`*"];
vecs = Join[RandomReal[{-1, 1}, {10^4, 2, 2}], {{{0, -1}, {0, 1}}, {{0, 1}, {0, -1}}}];

anglecalc1[u_, v_] := Mod[ArcTan[Dot[u, v], Det[{u, v}]], 2 Pi];
anglecalc2[u_, v_] := Mod[(2 UnitStep[Det[{u, v}]] - 1) VectorAngle[u, v], 2 Pi];

(* LLlAMnYP's method *)
anglecalc3[u_, v_] := Mod[(ArcTan @@ v) - (ArcTan @@ u), 2 Pi]

r1 = anglecalc1 @@@ vecs;
r2 = anglecalc2 @@@ vecs;
r3 = anglecalc3 @@@ vecs;

r1 - r2 // MinMax
r2 - r3 // MinMax

Output:

{-8.8817810^-16, 8.8817810^-16}
{-1.7763610^-15, 1.3322710^-15}

Original answer

anglecalc[u_, v_] := Mod[ArcTan[Dot[u, v], Det[{u, v}]], 2π]

or

anglecalc[u_, v_] := Mod[Sign[Det[{u, v}]] VectorAngle[u, v], 2π]

Really interesting to see an answer making use of VectorAngle, but the answer to this should be Pi, not zero: u = {0, -1}; v = {0, 1}; Mod[Sign[Det[{u, v}]] VectorAngle[u, v], 2 Pi] — Chris Degnen, May 08 '18 at 10:57

Better way to calculate angle between lines?

4 Answers4

Linked