Complex roots of a transcendental equation

Question

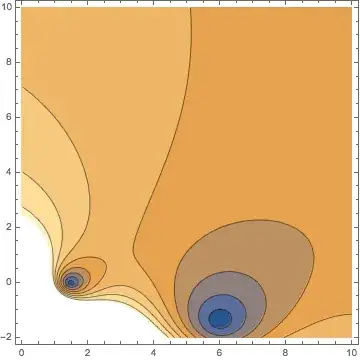
Let's define,

$k(e)=\sqrt{e}$, $\gamma_1(e,v_1,v_2)=(v_1+iv_2)/(i*k(e))$ , $\gamma_2(e,v_1,v_2)=(v_1-iv_2)/(i*k(e))$, $$\\$$ Now the function gets defined as, $f(e,v_1,v_2)=(2-\gamma_1(e,v_1,v_2)) (2-\gamma_2(e,v_1,v_2))-\gamma_1(e,v_1,v_2) \gamma_2(e,v_1,v_2)* e^{4 ik(e)}$

If I take, $v_1=1.4$, $v_2=2.2$, Then function $|f(e,v_1,v_2)|$ has a real root around 1.5, and I want know about its complex roots by any means.

Could you please help me ??

Here again rewrite above expressions,

k[e_]:=Sqrt[e];
gamma1[e_,v1_,v2_]:=(v1+I*v2)/(I*k[e]);
gamma2[e_,v1_,v2_]:=(v1-I*v2)/(I*k[e]);
f[e_,v1_,v2_]:=(2-gamma1[e,v1,v2])*(2-gamma2[e,v1,v2])-gamma1[e,v1,v2] *gamma2[e,v1,v2]* Exp[4*I*k[e]]

Provide your expressions as text-only Mathematica code in addition to $\LaTeX$ expressions. — MarcoB, May 06 '18 at 18:29
That is not sensible Mathematica code. Misused parentheses and underscore, to start. — John Doty, May 06 '18 at 18:36
"FindRoot[Abs[f[e,1.4, 2.2]]==0, {e=c+I]", where I am changing c, again by putting back the found root in Abs[f] to check, whether it goes zero on that root or not. — Schrodinger, May 06 '18 at 19:02
Related/duplicate: https://mathematica.stackexchange.com/questions/51115/find-all-roots-in-the-interval-of-nonlinear-equation — Michael E2, May 06 '18 at 21:28

Michael E2 · Answer 1 · 2018-05-06T21:10:50.537

If you bound the domain, NSolve can usually find all roots of an analytic function:

NSolve[f[e, 1.4, 2.2] == 0 && -10 < Re[e] < 10 && -10 < Im[e] < 10, e]
(*  {{e -> 1.46847 - 0.00315635 I}, {e -> 5.98286 - 1.3557 I}}  *)

You can make the domain somewhat larger:

NSolve[f[e, 1.4, 2.2] == 0 && 0 < Re[e] < 1000 && -100 < Im[e] < 100, e]
(*
{{e -> 1.46847 - 0.00315635 I}, {e -> 5.98286 - 1.3557 I}, {e -> 
   15.3143 - 4.22245 I}, {e -> 29.7131 - 7.79704 I}, {e -> 
   49.12 - 11.836 I}, {e -> 73.5089 - 16.229 I}, {e -> 
   102.866 - 20.9096 I}, {e -> 137.184 - 25.8326 I}, {e -> 
   176.457 - 30.9654 I}, {e -> 220.681 - 36.2831 I}, {e -> 
   269.854 - 41.7662 I}, {e -> 323.974 - 47.3988 I}, {e -> 
   383.038 - 53.1679 I}, {e -> 447.046 - 59.0626 I}, {e -> 
   515.996 - 65.0736 I}, {e -> 589.888 - 71.1928 I}, {e -> 
   668.721 - 77.4132 I}, {e -> 752.495 - 83.7288 I}, {e -> 
   841.208 - 90.134 I}, {e -> 934.86 - 96.6241 I}}
*)

score 3 · Accepted Answer · answered May 06 '18 at 19:43

Plotting suggests a root around 6-I.

ContourPlot[Abs[f[x + I y, 1.4, 2.2]], {x, 0, 10}, {y, -2, 10}]

FindRoot isn't very good for Abs[something]==0: it wants to see the function cross zero. Use FindMinimum:

FindMinimum[Abs[f[x + I y, 1.4, 2.2]], {{x, 6}, {y, -1}}]

After some complaining, it yields {1.30986*10^-7, {x -> 5.98286, y -> -1.3557}}, which may be good enough. Other roots, better roots, avoiding complaints, etc. left as an exercise for you.

Complex roots of a transcendental equation

2 Answers2