How can I do implicit differentiation in Mathematica

Question

I have the equation y*x + Sqrt[x^2 + 4*y] == 2. I need to calculate $dx/dy$ in $x=0$, $dx/dy$ in $y=1$, and also the tangent to that curve in $(0, 1)$

How do I do implicit differentiation? I've tried to do it the same way as normal differentiation but it doesn't work.

There is a search feature that can help find answers to such questions. — Michael E2, May 06 '18 at 20:53

Mariusz Iwaniuk · Answer 1 · 2018-05-06T20:42:22.147

eq = y x + Sqrt[x^2 + 4 y] == 2

Calculate: $dy/dx$

funcX = Dt[eq, x]
(* y + x Dt[y, x] + (2 x + 4 Dt[y, x])/(2 Sqrt[x^2 + 4 y]) == 0 *)
solX = Solve[funcX, Dt[y, x]]
(* {{Dt[y, x] -> (-x - y Sqrt[x^2 + 4 y])/(2 + x Sqrt[x^2 + 4 y])}}  *)

Calculate: $dx/dy$

funcY = Dt[eq, y]
(* x + y Dt[x, y] + (4 + 2 x Dt[x, y])/(2 Sqrt[x^2 + 4 y]) == 0 *)
solY = Solve[funcY, Dt[x, y]]
(* {{Dt[x, y] -> (-2 - x Sqrt[x^2 + 4 y])/(x + y Sqrt[x^2 + 4 y])}} *)

The equation of the tangent line at a regular point.

tangentcurve = (Dt[y, x] /. solX[[1]] /. x -> 0 /. y -> 1) (x - 
0) + (Dt[x, y] /. solY[[1]] /. x -> 0 /. y -> 1) (y - 1) == 0

(* 1 - x - y == 0 *)

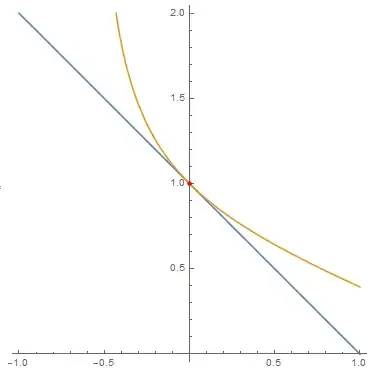
ContourPlot[Evaluate[{tangentcurve, eq}], {x, -1, 1}, {y, 0, 2}, 
Epilog -> {Red, PointSize[Medium], Point[{0, 1}]}, Axes -> True, 
Frame -> False]

Solve by normal differentiation:

EQx = y[x]*x + Sqrt[x^2 + 4 y[x]] == 2;
EQy = y*x[y] + Sqrt[x[y]^2 + 4  y] == 2;
SolX = Solve[D[EQx, x], y'[x]]
SolY = Solve[D[EQy, y], x'[y]]
TangentCurve = (y'[x] /. SolX[[1]] /. y[x] -> y /. x -> 0 /. 
y -> 1) (x - 0) + (x'[y] /. SolY[[1]] /. x[y] -> x /. x -> 0 /. 
y -> 1) (y - 1) == 0
ContourPlot[Evaluate[{TangentCurve, (EQx /. y[x] -> y)}], {x, -1, 1}, {y, 0, 2}, 
Epilog -> {Red, PointSize[Medium], Point[{0, 1}]}, Axes -> True, 
Frame -> False]

Do you agree it's a duplicate of the question I linked above? — Michael E2, May 06 '18 at 20:23
@MichaelE2. If got from you upvote then I will agree with you. — Mariusz Iwaniuk, May 06 '18 at 20:27

score 0 · Answer 2 · answered May 06 '18 at 20:03

(Dt[x, y] /. 
   First@Solve[Dt[y x + Sqrt[x^2 + 4 y] == 2, y], Dt[x, y]])
     /. {x -> 0, y -> 1}

Dt allows the taking of total derivatives. Using its second argument we can essentially take the total derivative with respect to y specifically, and then solve for the specific term Dt[x,y] which will remain, which is equivalent to $dx/dy$ in this case. Then we can substitute in {x -> 0, y -> 1} to get the result. You will want to change this substitution to get the other values you're interested in.

This agrees with direct differentiation:

xval = x /. Solve[y x + Sqrt[x^2 + 4 y] == 2, x];
Limit[D[xval, y], y -> 1]

Where one of the values is indeterminate because it refers to the wrong branch, but the other value is equivalent to the one acquired by implicit differentiation above.

How can I do implicit differentiation in Mathematica

2 Answers2