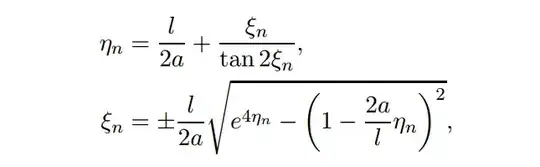plot the two functions in one picture for a/l=0.1 and give the code

Question

two functions i need to plot in one picture the required answer for a/l =0.1

Answer 1

$Version
(* "11.3.0 for Microsoft Windows (64-bit) (March 7, 2018)"*)
(* Executed in MMA 11.3 !!! *)

M = 1/10;(* a/l=1/10 *)
sol = NSolve[{n == 1/(2 M) + e/Tan[2 e], e == 1/(2 M)*Sqrt[Exp[4 n] - (1 - 2*M*n)^2], 
1/10 < e < 6, -1 < n < 1}, {e, n}] // Quiet

ContourPlot[{n == 5 + e/Tan[2 e], 
e == 5*Sqrt[Exp[4 n] - (1 - 2/10*n)^2]}, {e, 1/100, 6.3}, {n, -3, 
3}, ContourStyle -> {Black, {Dashed, Red}}, 
Epilog -> {RGBColor[0.2, 0.1, 0.8], Thickness[0.005], 
Table[Circle[{e /. sol[[k]], n /. sol[[k]]}, 0.07], {k, 1, 4}]}, 
Axes -> True, Frame -> False, PlotPoints -> 40, 
Prolog -> {Line[Table[{{k*Pi/2, -3}, {k*Pi/2, 3}}, {k, 1, 4}]]}]

---

Code for older version MMA:

Code findAllRoots2D from here:

$Version
(* 10.2.0 for Microsoft Windows (64-bit) (July 7, 2015) *)
(* Executed in MMA 10.2 !!! *)

ClearAll[findAllRoots2D];
Options[findAllRoots2D] = Join[Options[FindRoot], Options[Plot3D]];

findAllRoots2D[{f1_, f2_}, {x_, a_, b_}, {y_, c_, d_}, opts___] := 
Module[{f1plot, f2plot}, 
f1plot = 
Plot3D[f1, {x, a, b}, {y, c, d}, 
 MeshFunctions -> {Function @@ {{x, y}, f1}}, Mesh -> {{0}}, 
 PlotStyle -> None, PlotRange -> All, BoundaryStyle -> None, 
 Method -> Automatic, 
 Evaluate@FilterRules[{opts}, Options[Plot3D]]];
f2plot = 
ListLinePlot[
 Cases[Normal@f1plot, Line[pts_] :> pts[[All, {1, 2}]], Infinity],
  MeshFunctions -> {Function @@ {{x, y}, f2}}, Mesh -> {{0}}];
Quiet[Check[
   FindRoot[{f1 == 0, f2 == 0}, {x, #[[1]], a, b}, {y, #[[2]], c, 
     d}, Evaluate@FilterRules[{opts}, Options[FindRoot]]], 
   Unevaluated@Sequence[], FindRoot::reged], FindRoot::reged] & /@
 Cases[Normal@f2plot, Point[p_] :> p, Infinity]];

 M = 1/10;(*a/l=1/10*)
 f[n_, e_] := 1/(2 M) + e/Tan[2 e] - n;
 g[n_, e_] := 1/(2 M)*Sqrt[Exp[4 n] - (1 - 2*M*n)^2] - e;

 sol = findAllRoots2D[{f[n, e], g[n, e]}, {e, 1/10, 6}, {n, -1, 1}, 
 Method -> {"Newton", "StepControl" -> "LineSearch"}, 
 PlotPoints -> 85, WorkingPrecision -> 20]

 ContourPlot[{n == 5 + e/Tan[2 e], 
 e == 5*Sqrt[Exp[4 n] - (1 - 2/10*n)^2]}, {e, 1/100, 6.3}, {n, -3, 
 3}, ContourStyle -> {Black, {Dashed, Red}}, 
 Epilog -> {RGBColor[0.2, 0.1, 0.8], Thickness[0.005], 
 Table[Circle[{e /. sol[[k]], n /. sol[[k]]}, 0.07], {k, 1, 4}]}, 
 Axes -> True, Frame -> False, PlotPoints -> 40, 
 Prolog -> {Line[Table[{{k*Pi/2, -3}, {k*Pi/2, 3}}, {k, 1, 4}]]}]