2

This is essentially a follow-up question to this older post.

Given a configuration of tubes (or for simplicity cylinders), we draw them in a box using Graphics3D, where Tube is used for the particles and a Cuboid for the box. But in case the system has periodic boundary conditions, how should the drawing be done to include that in the output image? (Such as, one tube crossing one boundary on one side has the rest of it come out by the opposite side). I wonder if there are built-in features in Mathematica that can be used for such visualizations.

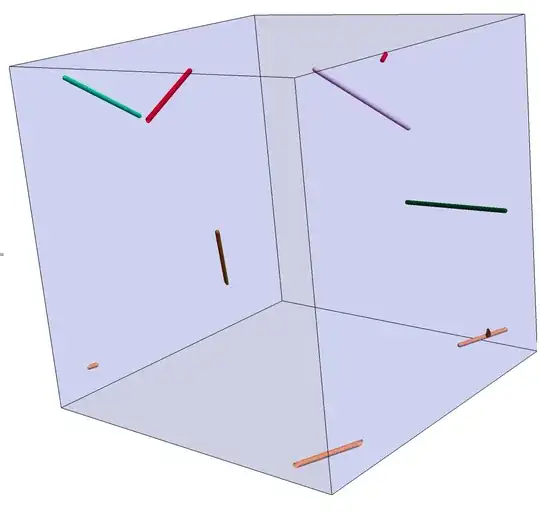
Dummy working example where we have some tubes sticking out of boundaries: a cubic box of 150 (in units of tube diameter which is set to one and length of tubes is 50), containing 6 tubes with following coordinates: (format: for each tube, we have two sets of coordinates for its end-points and its diameter.)

tubescoords = {{{36.5609, 76.3166, -54.0265}, {11.6599, 
54.1491, -16.7634}, {1}}, {{-36.2328, 11.7653, 
68.2118}, {-81.3504, -5.47683, 
55.2849}, {1}}, {{69.8237, -64.7285, -9.43758}, {67.6299,
-14.7808, -10.0801}, {1}}, {{-60.2174, 59.2337, 68.1819}, {-17.1851, 
65.5134, 43.5083}, {1}}, {{34.2708, -41.4081, 
33.4426}, {-1.21881, -23.1799, 
63.5793}, {1}}, {{-91.5513, -44.999, -71.719}, {-54.1793,
-76.8396, -62.2584}, {1}}}

So the box is: 

cube = Cuboid[-150/2 {1., 1., 1.}, 150/2 {1., 1., 1.}];

And to draw everything: 

Graphics3D[{
  CapForm[Round], Tube[{#1, #2}, #3] & @@@ tubescoords, 
  Blue, Opacity[0.1], cube
 }, 
 Boxed -> False
 ]
Michael E2
  • 235,386
  • 17
  • 334
  • 747
  • It would be nice if you could provide a simple example scene so that other users can play around with it. – Henrik Schumacher May 18 '18 at 10:00
  • @HenrikSchumacher good idea, please see the edit. –  May 18 '18 at 11:13
  • @HenrikSchumacher apparently Mod is sometimes used for these purposes, e.g. https://mathematica.stackexchange.com/questions/13113/3d-random-walk-with-periodic-boundary-conditions/13154 –  May 18 '18 at 12:46
  • I thought so. The problem with that is that your Tubes won't cross the boundary after applying Mod - Tubes follow always the shortest path between the end points and since the box is convex... So you have to create "mirror" points for Tubes and Lines that cross the boundary of the box. – Henrik Schumacher May 18 '18 at 12:49

1 Answers1

4

One way to do this would be to create copies of the tubes using GeometricTransformation, and then use the PlotRange to cut off what lies outside the boundary.

Here I'm adding a coloring to the tubes so that it's clear which tube stubs belong to each other.

tubescoords = {{{36.5609,76.3166,-54.0265},{11.6599,54.1491,-16.7634},{1}},
  {{-36.2328,11.7653,68.2118},{-81.3504,-5.47683,55.2849},{1}},
  {{69.8237,-64.7285,-9.43758},{67.6299,-14.7808,-10.0801},{1}},
  {{-60.2174,59.2337,68.1819},{-17.1851,65.5134,43.5083},{1}},
  {{34.2708,-41.4081,33.4426},{-1.21881,-23.1799,63.5793},{1}},
  {{-91.5513,-44.999,-71.719},{-54.1793,-76.8396,-62.2584},{1}}};
cube = Cuboid[-150/2 {1., 1., 1.}, 150/2 {1., 1., 1.}];
plotRange  = Thread@(List @@ cube);
dimensions = Subtract @@@ plotRange // Abs;
tubes = Tube[{#1, #2}, #3] & @@@ tubescoords;
(* adding in a coloring for visualizing periodicity *)
tubes = Thread[{RandomColor[Length @ tubes], tubes}];
transformations = TranslationTransform /@ Table[
    Sequence @@ {
      ReplacePart[{0, 0, 0}, n -> -dimensions[[n]]],
      ReplacePart[{0, 0, 0}, n -> dimensions[[n]]]
      },
    {n, 3}];
transformedTubes = GeometricTransformation[tubes, transformations];
Graphics3D[{CapForm[Round], tubes, transformedTubes, Blue, 
  Opacity[0.1], cube}, Boxed -> False, PlotRange -> plotRange]

enter image description here

Jason B.
  • 68,381
  • 3
  • 139
  • 286
  • Very interesting! Does this approach work for any of the boundaries crossed for the 3D box? –  May 18 '18 at 14:27
  • I believe so - I try rotating it with my mouse to verify. The code to generate the transformations could probably be written more clearly, to make it plain that I'm doing 6 translation transforms: ${\pm dx, \pm dy, \pm dz}$. – Jason B. May 18 '18 at 14:33
  • I think Quotient[RegionUnion @@ (Point[{#1, #2}] & @@@ tubescoords) // RegionBounds, 150, -150/2] tells you how many translates you need in each direction to tile a region covering the whole. (In case the paths extend farther than one box away.) – Michael E2 May 18 '18 at 14:47
  • @MichaelE2 very interesting! I was wondering, I know it s in 3D so may be harder, but is it possible to also draw next to the box it's first (nearest) periodic images? For example like this image (but it s 2D). –  May 20 '18 at 12:36
  • @user929304 You see one box because the PlotRange restricts the view to one box. So my first thought is to enlarge the PlotRange by ± one box, and see if you can adjust the graphics, if needed, to show what you want to illustrate. – Michael E2 May 20 '18 at 13:14
  • @MichaelE2 how can we modify the plotrange here? What I imagined was to replicate the box (with its current state) attached to each side (face) of the main box. –  May 20 '18 at 14:41
  • @user929304 The translates are already there in Jason's code. They're just cut out of the picture by the PlotRange. Start with PlotRange -> All, but you might want to modify plotRange in the code to suit your purposes. – Michael E2 May 20 '18 at 15:15