I define
ψ1 = Sqrt[Subscript[ρ, 1][t]] E^(I Subscript[θ, 1][t]);
ψ2 = Sqrt[Subscript[ρ, 2][t]] E^(I Subscript[θ, 2][t]);
and
eq1 = (I ℏ D[ψ1, t] - U ψ1 - K ψ2)/E^(I Subscript[θ, 1][t]) // FullSimplify
gives
I want to get the imaginary part of the above expression where $\rho$ is positive, and $\theta$ is real.
The result should be
while ComplexExpand gives
How do I do it correctly?
Try the following.
Here are your expressions:
ψ1 =
Sqrt[Subscript[ρ, 1][t]] E^(I Subscript[θ, 1][t]);
ψ2 =
Sqrt[Subscript[ρ, 2][t]] E^(I Subscript[θ, 2][t]);
eq1 =
(I*ℏ D[ψ1, t] - U ψ1 - k ψ2)/E^(I Subscript[θ, 1][t]) // FullSimplify
I assume, your K is not the reserved Mma constant and replaced it, therefore, by the small k above.
Let us now represent the exponent in the trigonometric form and replace the imaginary unit by any letter, say, by X for further use:
eq2 = ExpToTrig[eq1];
eq3=eq2 /. Complex[0, a_] -> X*a
Now this:
Coefficient[eq3, X]
makes the job:
Have fun!
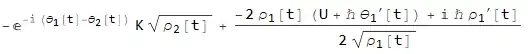
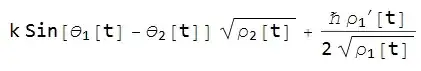
Subscript[ρ, 1][t] > 0andSubscript[ρ, 2][t] > 0, it works as expected – Lukas Lang May 30 '18 at 07:23Subscriptwhile defining symbols (variables).Subscript[x, 1]is not a symbol, but a composite expression whereSubscriptis an operator without built-in meaning. You expect to do $x_1=2$ but you are actually doingSet[Subscript[x, 1], 2]which is to assign a Downvalue to the operatorSubscriptand not an Ownvalue to an indexedxas you may intend. – rhermans May 30 '18 at 08:16