How to solve this trigonometric system?

Question

Namely,

$$\left\{\left(\tan ^2\left(x-\frac{\pi }{3}\right)+\tan ^2\left(y+\frac{\pi }{6}\right)\right) (\sin (x)+\cos (y)-1)=0,\\ (\sin (y)-\sin (2 y)+2) (\sin (x)-\cos (y))=0,\\x\geq 0,x<2 \pi ,y\geq 0,y<2 \pi \right\}. $$

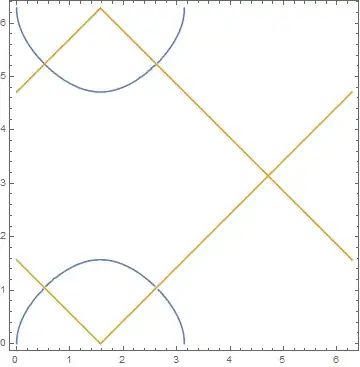
The plot

ContourPlot[{(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) ==0, 
(Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]) == 0}, {x,0,2*Pi}, {y, 0,2*Pi}]

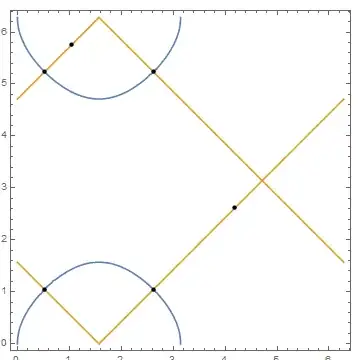
shows four real solutions. However,

Reduce[{(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 0, 
(Sin[x] -Cos[y])*(2 - Sin[2 y] + Sin[y])==0,x >= 0, x<2*Pi, y >= 0, y < 2*Pi},{x,y}, Reals]

performs

(x == [Pi]/6 && y == (5 [Pi])/3) || (x == 2 ([Pi] + ArcTan[Root[{-3 + #1^2 &, 9 + 24 #1 #2 + 168 #2^2 + 440 #1 #2^3 - 1604 #2^4 - 4968 #1 #2^5 + 8600 #2^6 + 11000 #1 #2^7 - 12042 #2^8 - 11000 #1 #2^9 + 8600 #2^10 + 4968 #1 #2^11 - 1604 #2^12 - 440 #1 #2^13 + 168 #2^14 - 24 #1 #2^15 + 9 #2^16 &}, {2, 2}]]) && y == 2 ArcTan[ Root[{-3 + #1^2 &, 9 + 24 #1 #2 + 168 #2^2 + 440 #1 #2^3 - 1604 #2^4 - 4968 #1 #2^5 + 8600 #2^6 + 11000 #1 #2^7 - 12042 #2^8 - 11000 #1 #2^9 + 8600 #2^10 + 4968 #1 #2^11 - 1604 #2^12 - 440 #1 #2^13 + 168 #2^14 - 24 #1 #2^15 + 9 #2^16 &, 31716 + 23256 #1 + 129132 #2 - 9873 #1 #2 + 3554904 #2^2 + 447978 #1 #2^2 - 3706428 #2^3 + 15729 #1 #2^3 - 23650076 #2^4 - 4305612 #1 #2^4 + 11333348 #2^5 + 7026787 #1 #2^5 + 46524792 #2^6 + 8877606 #1 #2^6 - 12884532 #2^7 - 11758723 #1 #2^7 - 44195412 #2^8 - 8512688 #1 #2^8 + 7284948 #2^9 + 9579965 #1 #2^9 + 19350440 #2^10 + 3611158 #1 #2^10 - 1247492 #2^11 - 1925981 #1 #2^11 - 1720692 #2^12 - 307100 #1 #2^12 + 116700 #2^13 + 219825 #1 #2^13 - 93816 #2^14 - 16998 #1 #2^14 + 6516 #2^15 + 11439 #1 #2^15 + 147456 #3 &}, {2, 2, 1}]]) || (x == 2 ArcTan[ Root[{-3 + #1^2 &, 9 + 24 #1 #2 + 168 #2^2 + 440 #1 #2^3 - 1604 #2^4 - 4968 #1 #2^5 + 8600 #2^6 + 11000 #1 #2^7 - 12042 #2^8 - 11000 #1 #2^9 + 8600 #2^10 + 4968 #1 #2^11 - 1604 #2^12 - 440 #1 #2^13 + 168 #2^14 - 24 #1 #2^15 + 9 #2^16 &}, {2, 6}]] && y == 2 [Pi] + 2 ArcTan[ Root[{-3 + #1^2 &, 9 + 24 #1 #2 + 168 #2^2 + 440 #1 #2^3 - 1604 #2^4 - 4968 #1 #2^5 + 8600 #2^6 + 11000 #1 #2^7 - 12042 #2^8 - 11000 #1 #2^9 + 8600 #2^10 + 4968 #1 #2^11 - 1604 #2^12 - 440 #1 #2^13 + 168 #2^14 - 24 #1 #2^15 + 9 #2^16 &, 31716 + 23256 #1 + 129132 #2 - 9873 #1 #2 + 3554904 #2^2 + 447978 #1 #2^2 - 3706428 #2^3 + 15729 #1 #2^3 - 23650076 #2^4 - 4305612 #1 #2^4 + 11333348 #2^5 + 7026787 #1 #2^5 + 46524792 #2^6 + 8877606 #1 #2^6 - 12884532 #2^7 - 11758723 #1 #2^7 - 44195412 #2^8 - 8512688 #1 #2^8 + 7284948 #2^9 + 9579965 #1 #2^9 + 19350440 #2^10 + 3611158 #1 #2^10 - 1247492 #2^11 - 1925981 #1 #2^11 - 1720692 #2^12 - 307100 #1 #2^12 + 116700 #2^13 + 219825 #1 #2^13 - 93816 #2^14 - 16998 #1 #2^14 + 6516 #2^15 + 11439 #1 #2^15 + 147456 #3 &}, {2, 6, 1}]])

which is not correct in view of

N[%]

(x==0.523599&&y==5.23599)||(x==4.18879&&y==2.61799)||(x==1.0472&&y==5.75959)

and

{(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) ==  0, 
(Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]) == 0} /. 
{x -> 4.188790204786391, y -> 2.6179938779914944}

{False,False}

Addition. Up to the suggestion of Michael E2, the command

Reduce[{(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 
0, (Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]) == 0, x>= 0, x < 2*Pi, y>= 0, y < 2*Pi}, {x, y}, Reals]//FullSimplify

does the job, outputting

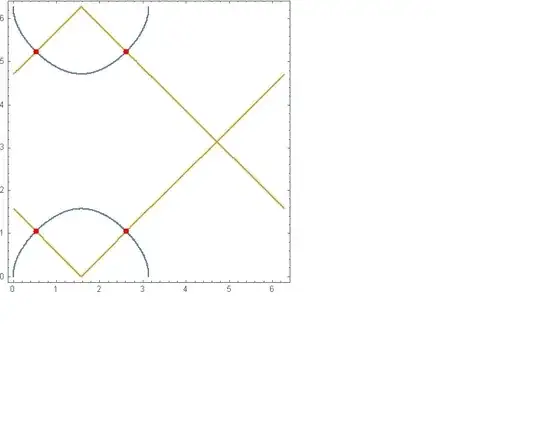
6 x == [Pi] && 3 y == 5 [Pi]) || (3 x == 4 [Pi] && 6 y == 5 [Pi]) || (3 x == [Pi] && 6 y == 11 [Pi])

Micael E2 also explains the result of ContourPlot in his comments.

The happy end.

Comments are not for extended discussion; this conversation has been moved to chat. — Kuba, Jun 01 '18 at 21:27

Henrik Schumacher · Answer 1 · 2018-05-31T11:40:39.627

The problem here is that by searching for roots of (Cos[y] + Sin[x] - 1) (Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2), we happen to have a root of the first factor where the second factor has a singularity. I am also not happy my the behavior of Reduce but I can understand that this is a delicate case.

Replacing the product by an Or (||) can serve as a somewhat dirty workaround:

eqn = {(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 
    0, (Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]) == 0};
eqn1 = {
  (Cos[y] + Sin[x] - 1) == 0 || (Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 0,
  (Sin[x] - Cos[y]) (2 - Sin[2 y] + Sin[y]) == 0, 
  0 <= x < 2 Pi, 
  0 <= y < 2 Pi
}; 
Reduce[eqn1, {x, y}] // RootReduce; 
sol = Solve[eqn1, {x, y}, Method -> Reduce]; 

pts = {x, y, 0} /. sol; 
Show[
 Graphics3D[{Red, Sphere[#, 0.2] & /@ pts}], 
 Plot3D[Evaluate@{eqn[[1, 1]], eqn[[2, 1]], 0}, {x, 0, 2*Pi}, {y, 0, 
   2*Pi}, PlotPoints -> 50, PlotRange -> {-2, 2}
  ],
 Axes -> True
 ]

Note also that two of the solution points do not appear in the contour plot because they are isolated roots of the first equation and thus hardly detectable by CountourPlot. (In the picture above, you see crossings of only green and blue or of only blue and yellow at these points.)

Let me recapitulate the discussion:

(1) OP complains that the solutions obtained from

f = (Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2);
g = (Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]);
cond = {f == 0, g == 0, x >= 0, x < 2*Pi, y >= 0, y < 2*Pi};
sol0 = Reduce[cond, {x, y}, Reals];

were wrong. But they aren't:

{f, g} /. Solve[sol0, {x, y}] // N

{{0., 0.}, {-1.33166*10^-31, 1.12111*10^-15}, {4.66608*10^-32, 5.25363*10^-16}}

So the solutions are correct up to machine precision (and that only because N was used). In fact, one could also use

{f, g} /. RootReduce[Solve[sol0, {x, y}]]

{{0, 0}, {0, 0}, {0, 0}}

(2) After getting this as feedback, OP complains in a comment that they want to have more roots ("more than four items").

But that enforces us to stretch the meaning of a solution and to include some extra solutions. mathe came up with the nice idea to use

sol = Solve[{Reduce[cond[[1 ;; 2]]], 0 <= x < 2 Pi, 0 <= y < 2 Pi}, {x, y}] // RootReduce;

Summarized this looks like this:

Show[
 ContourPlot[
  Evaluate@Join[{cond[[1 ;; 2]], y == Pi/3, x == 5/6 Pi}], {x, 0, 2 Pi}, {y, 0, 2 Pi}],
 Graphics[{PointSize[0.025], Point[{x, y} /. sol], Gray, 
   Point[{x, y} /. RootReduce[Solve[sol0, {x, y}]]]}]
 ]

Here the blue and yellow lines represent the zero-sets of f and g respectively, while the green and red line represent (a part of) the singular set of f. The three gray points are the three solutions from the beginning; the three black points came basically from the continuation of the zero-sets.

(3) OP complains that also the black points appear (although this was quite exactly what they asked for), downvotes and sends us back to high school.

If you ask me, something is really fishy about this procedure...

Thank you. You see the heart of the problem. However, I don't see a solution of the problem. Its solution by hand is not so hard. — user64494, May 31 '18 at 09:35
In what sense does this not solve the problem? Would you please be a bit more specific? The equation you have posted has precisely these six solutions. — Henrik Schumacher, May 31 '18 at 10:17
You solved the system which is not equivalent to the fomulated one: eqn /. sol[[1]] outputs {Indeterminate, 0}. The same issue with sol[[3]] and sol[[4]]. In fact you repeat the answer by @mathe. — user64494, May 31 '18 at 10:26
The system is equivalent to the orginal one. We just copied it from your post. Your means to check the solutions have flaws. ReplaceAll (/.) cannot compute limits. For example, compare ReplaceAll[Sin[x]/x /. x -> 0] and Limit[Sin[x]/x, x -> 0]. That's why I proposed to check your solutions with Reduce[eqn] /. sol instead. It returns {True, True, True, True, True, True}. — Henrik Schumacher, May 31 '18 at 10:29
Up to school math the points ${x= {\it arbitrary, real ,number}, y =\frac \pi 3 }$ do not belong to the domain of the system. — user64494, May 31 '18 at 10:40
No need to get patronizing towards people who spend their free time to help you. I'm done here. — Henrik Schumacher, May 31 '18 at 10:45

matrix42 · Answer 2 · 2018-05-31T09:55:06.670

7

I think this may be a bug with Reduce, but this works

eqn={(Cos[y]+Sin[x]-1) (Tan[x-Pi/3]^2+Tan[y+Pi/6]^2)==0,
     (Sin[x]-Cos[y]) (2-Sin[2 y]+Sin[y])==0};

sol=Solve[{Reduce[eqn],0<=x<2Pi,0<=y<2Pi},{x,y}]//RootReduce

ContourPlot[Evaluate[eqn],{x,0,2Pi},{y,0,2Pi},Epilog->{PointSize@Medium,Point[{x,y}/.sol]}]

{{x->π/6,y->π/3},{x->π/6,y->(5 π)/3},{x->π/3,y->(11 π)/6},{x->(5 π)/6,y->π/3},{x->(5 π)/6,y->(5 π)/3},{x->(4 π)/3,y->(5 π)/6}}

edited May 31 '18 at 09:55

answered May 31 '18 at 07:29

matrix42

6,996
2
26
62

Unfortunately, the command eqn/.sol[[1]] performs {Indeterminate == 0, True}. The same with sol[[4]] and sol[[5]]. -1 still is mine. – user64494 May 31 '18 at 09:32
@user64494 You are somewhat pushy, aren't you? Try Reduce[eqn] /. sol. I suggest to accept mathe's answer; it settles your original question as well as several follow-up questions. – Henrik Schumacher May 31 '18 at 09:46
@Henrik Schumacher: Sorry, I can't accept the solution of a different problem which is not equivalent to the fomulated one. – user64494 May 31 '18 at 10:07
@user64494 In what sense does this not solve the problem? Would you please be a bit more specific? The equation you have posted has precisely these six solutions – Henrik Schumacher May 31 '18 at 10:18
Up to school math the points ${ x={\it arbitrary,real,number},y=\pi /3 } $ do not belong to the domain of the system. Don't hesitate to ask for further explanation in need. – user64494 May 31 '18 at 10:43
1

Three of your solutions are correct. But at the two points where x = 5 Pi/6, Tan[x - Pi/3] is undefined. At the two lower points where y = Pi/3, Tan[y + Pi/6] is undefined. Therefore they are not solutions. If you enlarge the plot and omit the points, you'll see gaps at three of the points that indicate some sort of discontinuity, which corresponds to the points I indicated. – Michael E2 May 31 '18 at 13:28

score 2 · Answer 3 · edited May 31 '18 at 13:43

2

With some ConditionalExpression we found:

eqn = {(Cos[y] + Sin[x] - 1) (Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 0 && 
       (Sin[x] - Cos[y]) (2 - Sin[2 y] + Sin[y]) == 0};

sol = {x, y} /. N[Solve[{Reduce[eqn], 0 <= x < 2 Pi, 0 <= y < 2 Pi}, {x, y}]]
pts = sol[[1 ;; 4]];

ContourPlot[
  {(Cos[y] + Sin[x] - 1)*(Tan[x - Pi/3]^2 + Tan[y + Pi/6]^2) == 0,
   (Sin[x] - Cos[y])*(2 - Sin[2 y] + Sin[y]) == 0}, 
  {x, 0, 2*Pi}, {y, 0, 2*Pi}, PlotPoints -> 25, 
  Epilog -> {PointSize[Large], Red, Point[pts]}]

edited May 31 '18 at 13:43

MarcoB

67,153
18
91
189

answered May 31 '18 at 11:23

Gopal Verma

1,055
7
11

3

At the two points on the right, x = 5 Pi/6 and Tan[x - Pi/3] is undefined. At the two lower points, y = Pi/3 and Tan[y + Pi/6] is undefined. Therefore they are not solutions despite what the plot appears to show. – Michael E2 May 31 '18 at 13:05

How to solve this trigonometric system?

3 Answers3