How to deal with slow convergence of FindRoot

Question

As a simple example let's consider the function $f(x) = x \left(1-\frac{x}{3}\right) \left(\frac{x}{10}-1\right)$:

f[x_] := x (1-x/3) (x/10-1)

I want to find, $r(c)$, the root of the function $f(x)+c$ that is closer to $0$ for $c\in[0,1]$.

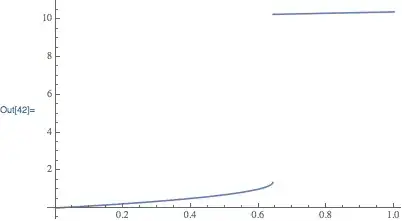
The value of the local minimum of $f$ is $c_{\text{min}}=-0.642389\dots$, this implies that for $c\le -c_{\text{min}}$, $r(c) < 1.38$ and for $c > -c_{\text{min}}$, $r(c) > 10.25$.

The problem of course is that if I call FindRoot with $0$ as the initial point,for $c=-c_{\text{min}}+\varepsilon$ the function $f(x)+c$ come close to the $x$ axis and the algorithm takes too long to converge.

Is there any way to tell mathematica that if it takes too long to find a root starting at 0, it should instead start at 10?

I would like to be able to plot the discontinuous function $r(c)$.

@AccidentalFourierTransform I forgot some minus signs. Sorry about that. I fixed it now. — tst, Jun 12 '18 at 14:09
Perhaps try NSolve[eq, x, Reals] and analyze the root closest to zero. Might depend on how complicated your actual $f(x)$ is. — Michael E2, Jun 12 '18 at 14:15

score 3 · Accepted Answer · answered Jun 12 '18 at 17:38

You can use NDSolveValue for a function that can't be handled with NSolve. Your function:

f[x_] := x (1-x/3) (x/10-1)

eqn = f[x[t]] + t == 0;

The corresponding ODE:

ode = D[eqn, t];
ode //TeXForm

$\left(1-\frac{x(t)}{3}\right) \left(\frac{x(t)}{10}-1\right) x'(t)+\frac{1}{10} \left(1-\frac{x(t)}{3}\right) x(t) x'(t)-\frac{1}{3} \left(\frac{x(t)}{10}-1\right) x(t) x'(t)+1=0$

To use NDSolveValue we will need initial conditions. Clearly:

t == -f[x[t]]

so we can use the initial conditions:

x[-f[0]] == 0

x[0] == 0

or

x[-f[11]] == 11

x[44/15] == 11

Now we are ready to use NDSolveValue:

left = NDSolveValue[
    {ode, x[-f[0]] == 0},
    x,
    {t, 0, 1},
    "ExtrapolationHandler" -> {Infinity&, "WarningMessage"->False}
];

right = NDSolveValue[
    {ode, x[-f[11]] == 11},
    x,
    {t, 0, 1}
];

min[t_] := Min[left[t], right[t]]

NDSolveValue::ndsz: At t == 0.6423882561207013`, step size is effectively zero; singularity or stiff system suspected.

(See @MichaelE2's answer to the question Suppress extrapolation of interpolating function in a ContourPlot for an explanation of the "ExtrapolationHandler" option)

Visualization:

Plot[min[t], {t, 0, 1}]

AccidentalFourierTransform · Answer 2 · 2018-06-12T14:31:54.147

0

Is this what you want?

Using

r[c_] := x /. NSolve[f[x] + c, x, Reals]
Show[
 Plot[r[c], {c, 0, 1/405 (-442 + 79 Sqrt[79])}], 
 Plot[r[c], {c, 1/405 (-442 + 79 Sqrt[79]), 1}]
, PlotRange -> All]

I get the plot

in under 0.3 seconds on my laptop.

To plot $r(c)$, just use

Plot[Min[r[c]], {c, 0, 1}, Exclusions -> {1/405 (-442 + 79 Sqrt[79])}]

which yields

as one would expect.

edited Jun 12 '18 at 14:31

answered Jun 12 '18 at 14:16

AccidentalFourierTransform

10,279
1
19
51

Well, yes, but I would like it to be possible without having explicit information about $f$. I know that my $f$ behaves like that locally, and I want the smallest positive root. – tst Jun 12 '18 at 14:41
Also NSolve cannot deal with any function and sometimes does not work. – tst Jun 12 '18 at 14:45

How to deal with slow convergence of FindRoot

2 Answers2