NIntegrate for extremely oscillatory function

Question

I have a question about how to use NIntegrate. I need to integrate a slightly different function thousands of times, one very much like the one I have posted below. The functions are highly oscillatory so I usually use the Cuba Vegas package, but I've been having so much difficulty getting Vegas to work consistently on my institute's research cluster that I'm thinking of going back to functions inherent to Mathematica. Another similar question on here had the answer to use Method -> "LevinRule", but in this case it takes hours and doesn't seem to get anywhere. Otherwise I can maybe just up the PrecisionGoal, but it will start taking a very long time... Vegas evaluates this very fast, to a good precision, is there anything similar in Mathematica?

Could anyone point me towards a quick and accurate integration strategy for this type of function please?

a = Sqrt[29.7/53.77];
NIntegrate[(((0.00025203302433875766 Exp[-(((Tan[x1]^2 + Tan[y1]^2)/
            5.8564 + (Tan[z1]^2)/1.9321)^(1/2))/
      a]) (Exp[-((((Tan[x1])^2 + (Tan[y1] - 0.4)^2)/
           5.8564 + ((Tan[z1])^2)/1.9321)^(1/2))/
     a]) (Exp[-((((Tan[x2] - 0.1)^2 + (Tan[y2] - 0.1)^2)/
           5.8564 + ((Tan[z2] - 0.1)^2)/1.9321)^(1/2))/
     a]) (Exp[-((((Tan[x2] - 0.1)^2 + (Tan[y2] - 0.1 - 0.4)^2)/
           5.8564 + ((Tan[z2] - 0.1)^2)/1.9321)^(1/2))/a]))/
Sqrt[(Tan[x1] - Tan[x2] + 0.1)^2 + (Tan[y1] - Tan[y2] + 
     0.1)^2 + (Tan[z1] - Tan[z2] + 0.1)^2])*

Sec[x1]^2 Sec[y1]^2 Sec[z1]^2 Sec[x2]^2 Sec[y2]^2 Sec[
    z2]^2, {x1, -Pi/2, Pi/2}, {y1, -Pi/2, Pi/2}, {z1, -Pi/2, 
  Pi/2}, {x2, -Pi/2, Pi/2}, {y2, -Pi/2, Pi/2}, {z2, -Pi/2, Pi/2}]

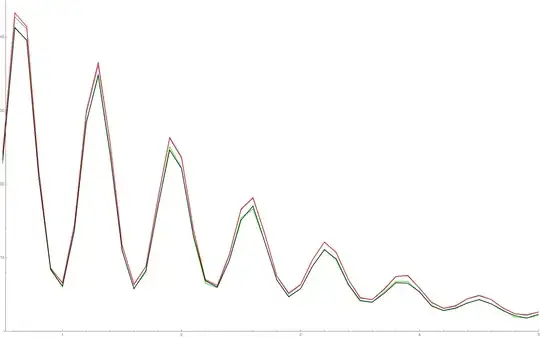
Here is an image of a couple of these integrations for similar functions (the x axis is just varying a constant so that we can see a couple of different results of the integration): Red - Vegas, Blue - MonteCarlo, Green - AdaptiveMonteCarlo, Black - MonteCarloRule

How do I know which of these is correct? AdaptiveMonteCarlo and MonteCarloRule both seem to be giving similar results which are lower than the similar results given by Vegas and MonteCarlo.

Thank you in advance.

Kind regards,

Ella

Can you show us the link for Cuba Vegas package? For this specific example, What's the result given by this package? How long does it take? — xzczd, Jun 17 '18 at 14:14
Cuba Vegas uses stochatic integration. So try out Method -> "MonteCarlo and friends. What is the precision you need for these integrals? — Henrik Schumacher, Jun 17 '18 at 14:35
xzczd, yes the link posted by MichaelE2. @HenrikSchumacher, thank you for putting me on the right track - I'm trying the MonteCarlo methods now and they are matching the results that I had obtained with Vegas. However, how should I choose between AdaptiveMonteCarlo (gives result 0.0106408 for the function in the post), MonteCarlo (0.0110414) or MonteCarloRule (0.0109079)? I have added a picture comparing the different methods in the question - how do I know which method is giving the most real result? Thank you though, everybody. — E Crane, Jun 17 '18 at 16:47
Hmm. Honestly. I don't know. If you require a high precision, NIntegrate will return a warning containing an error estimate. That error estimator seems to decay a bit faster with "AdaptiveMonteCarlo" with MaxPoints than the other stochastic methods: NIntegrate[f, {x1, -Pi/2, Pi/2}, {y1, -Pi/2, Pi/2}, {z1, -Pi/2, Pi/2}, {x2, -Pi/2, Pi/2}, {y2, -Pi/2, Pi/2}, {z2, -Pi/2, Pi/2}, Method -> {"AdaptiveMonteCarlo"}, MaxPoints -> 1000000, PrecisionGoal -> 4 ]. (f is your integrand`.) — Henrik Schumacher, Jun 17 '18 at 17:21
With MaxPoints -> 1000000, the three leading digits seem to be correct (relative error is 0.43 permille). But that needs 25 seconds for evaluation. MaxPoints -> 100000 leads to an relative error of 7 permille within 0.25 seconds. So, as always, you have to trade speed versus accuracy. — Henrik Schumacher, Jun 17 '18 at 17:26
Please can you send me some codes or examples how to use vegas in mathematica. I need it badly to save time for my codes, i am using NIntegrate to calculate , it takes more time. Please send me the links about how to use vegas with some examples . My email id is immy.salam@gmail.com Fervently looking for your response , it will be of immense help With Regards — Immy Salam, Jan 05 '20 at 18:54

score 5 · Accepted Answer · answered Jun 17 '18 at 17:43

The integrand is not oscillatory, but it is very high-dimensional. It does decay rather quickly at the boundary. (After an arctangent substitution, all the trig. functions go away and we have a exponentially decaying integral over ${\bf R}^6$.)

One can raise "MaxErrorIncreases" as suggested in the warning message or use Method -> "LocalAdaptive". By raising "MaxErrorIncreases", the integral converges: the error intervals are nested and decrease in length, but somewhat slowly. The "LocalAdaptive" method gives a result without warning messages but one that is somewhat different than the "GlobalAdaptive" method.

For a call of the following form, where i0 is the OP's integrand and "MaxErrorIncreases" -> 10000 may be set to whatever number, the results are summarized in the table below the call:

NIntegrate[i0,
  {x1, -Pi/2, Pi/2}, {y1, -Pi/2, Pi/2}, {z1, -Pi/2, Pi/2},
  {x2, -Pi/2, Pi/2}, {y2, -Pi/2, Pi/2}, {z2, -Pi/2, Pi/2},
  Method -> {"GlobalAdaptive", "MaxErrorIncreases" -> Incr}] // AbsoluteTiming

Incr    Integral     Error          Interval                    Timing
  2000  0.000807653  5.03281*10^-5  {0.000757325, 0.000857981}     9.31232
 10000  0.000795684  1.51190*10^-5  {0.000780565, 0.000810803}    49.7873
 50000  0.000792272  3.10038*10^-6  {0.000789172, 0.000795372}   259.574
200000  0.000791696  7.78874*10^-7  {0.000790917, 0.000792475}  1043.42

The "LocalAdaptive" result does not lie in all the above intervals:

NIntegrate[i0,
  {x1, -Pi/2, Pi/2}, {y1, -Pi/2, Pi/2}, {z1, -Pi/2, Pi/2},
  {x2, -Pi/2, Pi/2}, {y2, -Pi/2, Pi/2}, {z2, -Pi/2, Pi/2},
  Method -> "LocalAdaptive"] // AbsoluteTiming
(*  {84.5794, 0.000806581}  *)

If the arc tangent substitution is made, I get a slight better result after a longer computation:

(*  {258.019903, 0.0007963143048912211}  *)

Thank you very much @MichaelE2. Why is Global or Local adaptive methods a better choice than MonteCarlo methods here? Also you seem to know which gives the best result by looking at the error, is there a simple way to display the error so that I can also compare strategies - in another answer you posted something to do with IntegrationMonitor? — E Crane, Jun 17 '18 at 18:15
@ECrane The error estimates are reported in the NIntegrate::eincr warning message, but you can also get it from IntegrationMonitor. I get messages in all four "GlobalAdaptive" cases, so reading the error off the messages was easiest. I don't have a good understanding of the strengths and weaknesses of Monte Carlo, except they are recommended for high-dimensional integrals because everything else often fails. Here we have a function that decays at the boundary, so I felt the standard multidimensional rule had a chance.... — Michael E2, Jun 17 '18 at 18:59
There is a singularity where the Sqrt in the denominator vanishes. You can point out the singular manifold to NIntegrate but the computed value of the integral seems stable. So I think that NIntegrate is handling the singularity satisfactorily. Admittedly I'm just relying on some heuristic evidence for this conclusion. — Michael E2, Jun 17 '18 at 19:02

NIntegrate for extremely oscillatory function

1 Answers1