I am trying to solve the following reaction-diffusion equation where R_L represents the reaction rate of L.
Clear["Global`*"]
k1 = 0.00193*10^-9;
k2 = 0.00255*10^-9;
k3 = 4.09*10^-9;
d1 = 0.00700;
d2 = 3.95*^-5;
d3 = 2.26;
K1 = 3.63*10^-9;
K2 = 0.155*10^-9;
K3 = 0.553*10^-9;
K4 = 9.01*10^-12;
Ki = 0.139;
NT = 1.70*10^-12;
L0 = 1*10^-9;
n = (200*^9)/(1.3*^-9);
NA = 6.02*^23;
r = -(K3*K4*
Ki*(K2 +
L[x] - ((8*K2*NT*L[x]^2 + K3*K4*Ki*L[x]^2 + 8*K2*K3*NT*L[x] +
K2^2*K3*K4*Ki + 8*K2^2*K3*Ki*NT + 2*K2*K3*K4*Ki*L[x] +
8*K2*K3*Ki*NT*L[x])/(K3*K4*Ki))^(1/2)))/(4*(K3*L[x] +
L[x]^2 + K2*K3*Ki + K3*Ki*L[x]));
R = (L[x]/K1);
rr = (1/K4) r^2;
rR = (L[x]/((2*K2)*K4)) r^2;
pR = (L[x]/((2*K2)*K4*Ki)) r^2;
RR = (L[x]^2/(K2*K3*K4*Ki)) r^2;
r = (-(1 + (L[x]/
K2)) + \[Sqrt]((1 + (L[x]/
K2))^2 - (4*((2/
K4)*((1 + (L[x]/
K2))*((1 + (1/
Ki))*((1 + (L[x]/K3))))))*(-NT))))/(2*((2/
K4)*((1 + (L[x]/K2))*((1 + (1/Ki))*((1 + (L[x]/K3)))))));
myL = ((2*d1*(NT - r - rr - rR - pR - RR)) - (2*k1*L[x]*r)) + ((2*
d2*(NT - r - R - rr - pR - RR)) - (k2*
L[x]*(NT - r - R - rR - pR - RR))) + ((d3*(NT - r - R - rr -
rR - pR)) - (2*k3*L[x]*(NT - r - R - rr - rR - RR)))
(*---------------------------------------------------------------*)
diffCo = 1*10^-6;
bc = {L[0] == 1, L[100] == 0};
eqn = diffCo*L''[x] + myL == 0;
solNDSolve =
NDSolve[{eqn, bc}, L, {x, 0, 100},
Plot[solNDSolve[x], {x, 0, 100}, PlotRange -> Full]
I originally used
bc = {DirichletCondition[L[x] == 1, x == 0],
DirichletCondition[L[x] == 0, x == 100]};
which gave me back the errors:
CoefficientArrays::poly: -((0.00106107 L (-1-6.45161 L+Sqrt[12.3687 (1+Times[<<2>>]) (1+Times[<<2>>])+(1+Times[<<2>>])^2]))/((1+1.80832 L) (1+6.45161 L)))+2.26 (<<1>>)-0.00255 L (<<1>>)+0.014 (<<1>>)+0.000079 (<<1>>)-8.18 L (<<1>>)+L$45220/1000000 is not a polynomial.
and
NDSolve::femper: PDE parsing error of {-((0.00106107 L (-1-6.45161 L+Sqrt[12.3687 (1+Times[<<2>>]) (1+Times[<<2>>])+(1+Times[<<2>>])^2]))/((1+1.80832 L) (1+6.45161 L)))+<<7>>+L$45220/1000000}. Inconsistent equation dimensions.
when I switched it to
bc = {L[0] == 1, L[100] == 0};
I don't get the error message anymore, however, now it just runs without stopping/giving any error messages.
Solving using FEM doesn't seem to be working. Is there another way to solve this problem without using FEM?

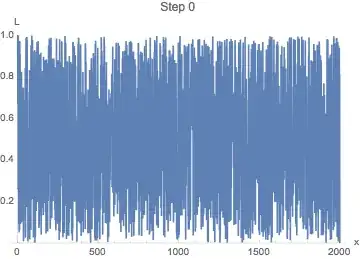
bc = {L[0] == 1, L[100] == 0};) and removing theMethodcall insideNDSolve, it at least tries to evaluate. However, it ran for a few minutes on my computer without returning a result, probably because of the complexity of the problem, and I aborted it. Perhaps you can wait longer and see. – MarcoB Jun 18 '18 at 23:25So, does this mean that the FEM method is not compatible with my problem? Is there a way to have it solve using another method?
– BaiSango Jun 19 '18 at 04:37NDSolveto give you a better answer. There is, however, A LOT of information on this site on solving differential equations in general, and on FEM as well. I suggest a deep dive into some older answers first. – MarcoB Jun 19 '18 at 04:45Plotwon't work even if you successfully solve the equation, for more information, check document ofNDSolveandReplaceAllcarefully. Then,NDSolveis very slow on this problem because the solution is severely oscillating, try e.g.sol = NDSolveValue[{eqn, L[0] == 1, L'[0] == 0.1}, L, {x, 0, 100}]; Plot[sol[x], {x, 0, 0.2}]Is it suppose to be like this? If not, you should double check the underlying model. – xzczd Jun 19 '18 at 06:01NDSolve. Even if it were, one thing that is missing is an initial guess of L[x]. Also, are you sure the equations are correct? – user21 Jun 19 '18 at 08:51