Find the intersection of functions given by lists

Question

How can the intersection of two functions that their values are given by lists. For example:

list1 = Table[Cos[x], {x, 0, 10, 0.5}]
list2 = Table[0.1 x, {x, 0, 10, 0.5}];
Show[ListLinePlot[list1], ListLinePlot[list2]]

or a simpler case, when one of the lists intersects zero.

Can your lists have the abscissa values as well as the ordinates (I.e. Table[{x, Cos[x]}, {x, 0, 10, 0.5}]? — MarcoB, Jun 21 '18 at 16:57

score 3 · Answer 1 · answered Jun 21 '18 at 17:07

Let's construct interpolations of your lists:

list1 = Table[{x, Cos[x]}, {x, 0, 10, 0.5}];
list2 = Table[{x, 0.1 x}, {x, 0, 10, 0.5}];

interpolations = Interpolation /@ {list1, list2};

I am then going to use an NDSolve-based approach to find all intersection, by finding zeroes of the difference between the two interpolating functions:

Clear[f]
f[x_] := Subtract @@ Through[interpolations[x]]

sol = Reap@
   NDSolve[{
     D[y[x], x] == D[f[x], x], y[1] == f[1],
     WhenEvent[y[x] == 0, Sow[x]]},
    y, {x, 3, 10}
    ];

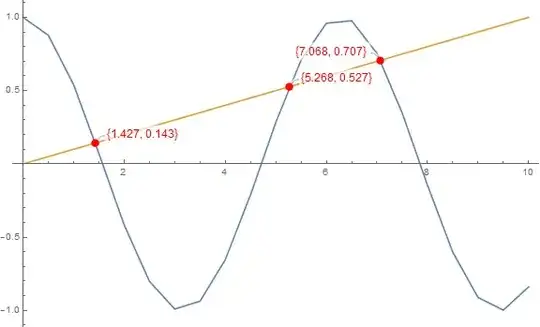
The result contains the abscissae of the intersection points:

sol[[2, 1]]
(* Out: {1.42738, 5.2681, 7.06842} *)

Let's plot these points to check that this approach is sound:

Show[
 ListLinePlot[{list1, list2}, ImageSize -> Large],
 ListPlot[
   Callout[
     {#, interpolations[[1]][#]},
     Round[{#, interpolations[[1]][#]}, 0.001],
     LabelStyle -> Directive[Red, Medium]
     ] & /@ sol[[2, 1]
   ], PlotStyle -> {Red, PointSize[0.015]}
 ]
]

Mathematica graphics

It looks rather complicated, and I'd like to avoid interpolations, I'll wait for another answer, and if there'll be none I'll accept your answer. — jarhead, Jun 21 '18 at 17:24
Maybe it's better to start with the simple case, of a list that intersects zero — jarhead, Jun 21 '18 at 17:24
@jarhead Why would you like to avoid interpolations? Perhaps if we knew more about the underlying problem, we could propose a better solution. — MarcoB, Jun 21 '18 at 18:27

score 1 · Accepted Answer · answered Jun 21 '18 at 19:50

I would have used interpolation myself. If you don't want to interpolate (that means use the data point only) then you can look for where the difference of of the functions changes sign. This method depends on the two functions being evaluated at the same points, which from your definitions seems to be true. I'll include the x values as per the comments:

list1 = Table[{x, Cos[x]}, {x, 0, 10, 0.5}];
list2 = Table[{x, 0.1 x}, {x, 0, 10, 0.5}];
difflist = Transpose[{First /@ list1, (Last /@ list1) - (Last /@ list2)}];
intersections = Table[If[difflist[[i, 2]]*difflist[[i + 1, 2]] < 0, {difflist[[i, 1]], list1[[i, 2]]}, Nothing], {i, Length[difflist] - 1}];

Since we cannot know where between point $i$ and point $i+1$ the intersection lies, I've just used the value at $i$. You can do other things here if you like.

Find the intersection of functions given by lists

2 Answers2