How is this series not converging properly?

Question

I have a function $g(x)$ that looks like this:

ListPlot[Table[{x, g[0.5, x, 3, 1]}, {x, -15, 15, 0.1}], 
   Joined -> True, ImageSize -> Large, InterpolationOrder -> 2, 
   PlotRange -> All] // AbsoluteTiming

I am trying to calculate the following integral:

$$\int_{-\infty}^{\infty} \cos (5.5x) g(x) \,dx \tag{1}$$

Naturally, to speed up convergence, I would like to limit the integration to a smaller domain than $(-\infty,\infty)$, which you can see should be justified by the fact that $g(x)$ quickly dies off past $x=5$. So I calculated (1) with the following limited domain:

$$\int_{-L}^{L} \cos (5.5x) g(x) \,dx \tag{2}$$

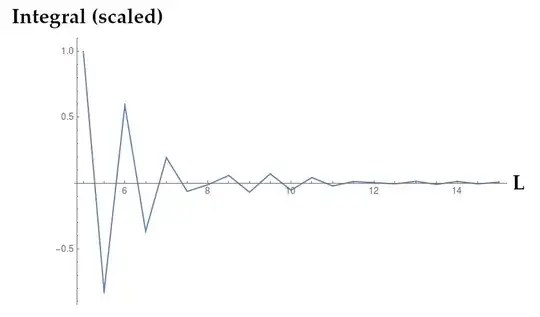
for increasing values of $L$. Once again, just by looking at the plot of $g(x)$ above, the majority of the integral should come from $-5<x<5$, so I would expect some reasonable convergence. But this is not what I found. In the plot below

testlength = 
  Table[{L, NIntegrate[Cos[5.5*y]*g[0.5, y, 3., 1.], {y, -L, L}]}, {L,
     5., 15., 0.5}]; (*checking convergence in interval size, t=5.5*)

ListPlot[{#[[1]], #[[2]]/2.1571002369282504`*^-6} & /@ testlength, 
  Joined -> True, ImageSize -> Large, PlotRange -> All, 
  AxesLabel -> {"L", ""}]

The integral is oscillating symmetrically about $0$ (I checked), and quickly dying off. What's going on here? How is this possible?

---

Supporting Code:

ClearAll[g];
g[x_?NumericQ, En_?NumericQ, pz_?NumericQ, \[Alpha]_?NumericQ] := 
  1./(En^2 + pz^2 + 0.24^2)*
   NIntegrate[((Sqrt[
       0.316/(1. + 
          1.2*((k4 + 0.5*En)^2 + kp + (x*pz)^2))^\[Alpha]*0.316/(1. + 
          1.2*((k4 - 0.5*En)^2 + 
             kp + ((1. - x)*pz)^2))^\[Alpha]])*((1. - x)*0.316/(1. + 
          1.2*((k4 + 0.5*En)^2 + kp + (x*pz)^2))^\[Alpha] + 
       x*0.316/(1. + 
          1.2*((k4 - 0.5*En)^2 + 
             kp + ((1. - x)*pz)^2))^\[Alpha]))/(((k4 + 0.5*En)^2 + 
       kp + (x*pz)^2 + (0.316/(1. + 
          1.2 ((k4 + 0.5*En)^2 + kp + (x*pz)^2))^\[Alpha])^2)*((k4 - 
         0.5*En)^2 + 
       kp + ((1. - x)*
         pz)^2 + (0.316/(1. + 
          1.2*((k4 - 0.5*En)^2 + 
             kp + ((1. - x)*
               pz)^2))^\[Alpha])^2)), {k4, -\[Infinity], \
\[Infinity]}, {kp, 0, \[Infinity]}, Method -> "LocalAdaptive"];

Answer 1

It's converging just fine. The function being integrated looks like this:

Just eyeballing it, it looks quite plausible that the integral could be zero. There is in fact a delicate cancellation as you add more oscillations.

Here is a smoother version of your plot of the integral. (I made a large table of g values from -30 to 30 in steps of 0.01, and used Interpolation to make a function out of that. That allows for much faster experimentation.)

If I step the bounds of the integral out to the places where the integrand hits zero from above (blue) and the below (orange), out to -30 to +30, I see this in a log plot of the absolute values of the integrals:

Which looks like it’s converging nicely to zero down to below $10^{-7}$. Sometime after that the negative integrals go positive (after the bounds -21 to +21) and they both converge to a very small positive value, probably due to the inherent error in the interpolation, or in the calculation of g itself. That could be resolved with higher precision experimentation.

Update:

I tried ten times as many points in the interpolation, and I got exactly the same behavior. So it might actually converge to that small number ($\approx 3\times 10^{-9}$), subject to the accuracy of the numerical integrations used to calculate g in the first place.

Answer 2

Some observations. First of all, the function g(x) resembles a Gaussian. It looks proportional to $exp(-x^2/6)$ from the picture. Therefore the integrand $\cos(55/10\ x)\ g(x)$ is an even function, so its symmetric integral cannot be zero.

The integration between $-L$ and $L$ gives a result proportional to

(I Sqrt[(3 \[Pi])/2] (Erfi[(33 - 2 I L)/(2 Sqrt[6])] - Erfi[(33 + 2 I L)/(2 Sqrt[6])]))/E^(363/8)

This function oscillates wildly. The function proportional to the last one

I*(Erfi[(33 - 2 I L)/(2 Sqrt[6])] - Erfi[(33 + 2 I L)/(2 Sqrt[6])])

stabilises at around $L=20.0$, giving the value of $2.0$ according to Mathematica.