How to creat a pyramid like grid?

Question

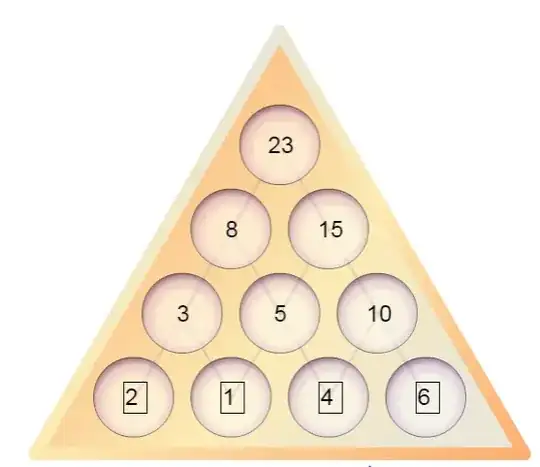
I'd like to create some pyramid that looks like this,

The numbers/cells are easy to do

Grid[NestWhileList[ Table[#[[i]] + #[[i + 1]], {i, 1, Length[#] - 1}] &, {1, 22, 5, 7}, Length[#] > 1 &] // Reverse, Frame -> All]

Grid[NestWhileList[ Table[#[[i]] + #[[i + 1]], {i, 1, Length[#] - 1}] &, {a, b, c, d},    Length[#] > 1 &] // Reverse, Frame -> All]

But then the output is not quite there yet. Easily achievable?

You can also make use of some triangle lattice functionality from IGraph/M, even though it's not made for this. http://i.stack.imgur.com/SpEH0.png — Szabolcs, Jun 25 '18 at 21:03
@Szabolcs It does not seem to be able to do the "triangular" style frame, but that's fine. Thanks. Column[Grid[{#}, ItemSize -> 3] & /@ (NestWhileList[ Table[#[[i]] + #[[i + 1]], {i, 1, Length[#] - 1}] &, {1, 22, 5, 7}, Length[#] > 1 &] // Reverse), Center, Frame -> All] — Chen Stats Yu, Jun 25 '18 at 21:17
https://thinkmeta.wordpress.com/2010/06/28/scala-expressiveness/ — matrix42, Jun 26 '18 at 10:09

rhermans · Accepted Answer · 2018-06-26T08:20:51.680

fun[f_, list_] := NestList[
  f @@@ Partition[#, 2, 1] &,
  list
  , Length[list] - 1
  ]

build[list_] := Module[
  {
   coordinates = 
    Flatten[
     MapIndexed[
      {#1, First[#2]} &, 
      fun[(#/2) &@*Plus, Range[Length[list]]],
      {2}
      ],
     1
   ],
   numbers = Flatten[fun[Plus, list]]
   },
  Graphics[
   {LightOrange,
    Disk[#, 0.4] & /@ coordinates,
    Black,
    Thread@Text[numbers, coordinates]
    }
   ]]


build[{2, 1, 4, 6}]

Mathematica graphics

How to creat a pyramid like grid?

1 Answers1