Area of volume of revolution

Question

I want to calculate the exact area of this volume:

RevolutionPlot3D[
 f[x_] = Sqrt[28 x]
 , {x, 0, 21}
 , Axes -> True
 ]

Additionally, I wish to see $x$ and $y$ axis.

Before you vote down my question because I don't know how mathematica works and dare asking, I did try to solve it in the documentation. But that page does not reply to my question.

Area[f[x]]

gives output

Area::reg: 20.105968871208372` is not a correctly specified region. Area[20.106]

Thanks for accepting my answer, but I think you were too hasty doing that. While accepting is one of the things to do after your question is answered, we recommend that all users should test answers before voting and wait 24 hours before accepting the best one. That allows people in all timezones to answer your question and an opportunity for other users to point alternatives, caveats or limitations of the available answers. — rhermans, Jun 27 '18 at 08:19
It's up to you, you could un-check now and come back tomorrow and accept the best answer then, or you could just take the idea and apply it in the future. — rhermans, Jun 27 '18 at 08:26
I take the idea then. Your code works beautifully so seems unfair to uncheck. — Dovendyr, Jun 27 '18 at 08:33

score 10 · Answer 1 · answered Jun 27 '18 at 08:13

10

r = ParametricRegion[{r Cos[ϕ], Sin[ϕ] r, 
    Sqrt[28 r]}, {{r, 0, 21}, {ϕ, 0, 2 π}}]

Area[r]

49/2 π (14 Sqrt[3] - ArcSinh[Sqrt[3]])

answered Jun 27 '18 at 08:13

Rom38

5,129
13
28

Thank you, Rom38! That was also short and neat. – Dovendyr Jun 27 '18 at 11:46

rhermans · Accepted Answer · 2018-06-27T08:23:05.800

It seems that f[x] is evaluating to a number. Probably you Set an OwnValues for x? Check by evaluating ?x.

Area is only defined for regions, parametric surfaces and sets of coordinates, not single numbers nor plots.

Therefore, my the strategy is to first, start with a fresh kernel. Then, create a Cartesian parametric expression for the surface and use Area on that.

To create the parametric expression in Cartesian coordinates the easiest way is to start with the cylindrical coordinantes {r, θ, f[r]} and then use CoordinateTransform

CoordinateTransform[
 "Cylindrical" -> "Cartesian"
 , {r, θ, Sqrt[28 r]}
]

See also this other answer using ParametricRegion.

Here my take on it.

With[
 {
  parmcartsn = CoordinateTransform[
    "Cylindrical" -> "Cartesian"
    , {r, θ, Sqrt[28 r]}
    ]
  },
 Column[
  {
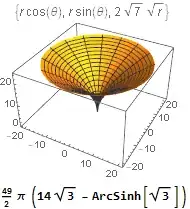
   ParametricPlot3D[
    parmcartsn
    , {r, 0, 21}
    , {θ, 0, 2 π}
    , PlotLabel -> TraditionalForm[parmcartsn]
    ],
   Area[
    parmcartsn
    , {r, 0, 21}
    , {θ, 0, 2 π}
    ]
   }
  ]
 ]

Mathematica graphics

Thank you. I would have never come to that answer. I don't know how to parametrize with cos and sin, how can I do it with an easy f(x) function? — Dovendyr, Jun 27 '18 at 08:15
Let me try that thing ''cartesian to parametric'' with another math problem. I'll post a new question if I'm lost... — Dovendyr, Jun 27 '18 at 08:43

user58973 · Answer 3 · 2018-06-28T15:05:48.970

1

Maybe I'm missing something but shouldn't $ f(x) = \sqrt{28 x} $ yield a concave function as opposed to the convex examples shown in the anwers above? My approach would be to use the formula for Solids of Revolution : $$ V=\pi \cdot \int_{a}^{b}f(x)^{2}dx $$ analogous to $V = \pi r^2\cdot h$ for a cylindrical body where $r$ is the radius and $h$ is the cylinder height. This, evaluated by Mathematica or otherwise (I did it quick'n dirty by hand, so I hope I didn't make an error) should give: $$ \pi \cdot 12348 \approx 38792.39 $$

After misunderstanding the question at first, mistakenly stopping at giving the Volume of the Solid of revolution, the addendum for the surface area follows here: Further reading in the wikipedia article linked above also gives a pretty simple equation for the surface area with respect to rotation around the x-axis: $$ S = 2 \pi \int_{a}^{b} f(x) dx $$ in analogy to $S = 2\pi r \cdot h$ for a cylindrical body. Because an exact result is required, I'll stop short of giving an value, as square roots are involved. But it should be easy enough from here.

edited Jun 28 '18 at 15:05

answered Jun 27 '18 at 09:50

user58973

19
2

The exercise is to calculate an area so I don't know if it applies.... – Dovendyr Jun 27 '18 at 09:51
yeah, 'area of volume' in the OP sounds a bit confusing. I think the above approaches somehow include an axis swap from x to y. This may be perfectly reasonable, though I..don't really get it. – user58973 Jun 27 '18 at 10:10
Your formula gives a volume; the question is the area of the volume, like its skin (?). Don't know what the correct English expression would be. – Dovendyr Jun 27 '18 at 11:43
oh, the surface area? Yeah, in that case, my solution won't help – user58973 Jun 27 '18 at 12:56
thanks for trying to help in any case! – Dovendyr Jun 27 '18 at 18:03
thought a bit about that further; the Area should also be calculat-able with pretty elementary means. Will probably update my answer for that. – user58973 Jun 28 '18 at 14:44
voted you up :)! – Dovendyr Jul 03 '18 at 05:18

Area of volume of revolution

3 Answers3

Linked