3

When writing out some mathematical equation like we see on the picture here I got the problem of writing out all terms. I know what recursion means and have done recursion for example for the Fibonacci sequence as we see here:

f[0] = 0;
f[1] = 1;
f[n_] := f[n] = f[n - 1] + f[n - 2]

But obviously it is harder in my problem. So first of all I defined the generating function (in the paper this is $\phi_p (z)$.):

 A[z_,p_] = ((1-p) + pz)^2;

which results in (In the paper this is $G_n(z)$):

 G[n_,z_,p_] = A[z,p]^(2^n - 1) G[n-1, A[z,p] / A[z,1-p] ,p]

as we can see in the image below.

The problem is to compute this until $n=0$, I need to substitute at each step. For example if I want to go to $n-2$ i will set u = A[z,p] / A[z,1-p], where in the paper $u = s_{n-1} (z)$, futhermore note that $q_1 = 1-q_{-1}$ then we get:

 G[n_,z_,p_] = A[z,p]^(2^(n - 1)) G[n-1,u,p]

$G_n(z) = \phi_{q{-1}}^{2^{n-1}}(z) G_{n-1}(s_{n-1}(z))$

 G[n_,z_,p_] = A[z,p]^(2^(n - 1)) A[u,p]^(2^(n - 2)) G[n-2,u,p]

$G_n(z) = \phi_{q{-1}}^{2^{n-1}}(z) \phi_{q{-1}}^{2^{n-2}}(u) G_{n-2}(s_{n-2}(z))$

Thus it is some recursion with a substitution in each step. My main question is

How should I perform the substitution on each step so in the end i get some closed form dependent on only the variable $z$?

If one can do this one just needs to calculate the derivatives to get an analytical solution for the probabilities:

https://en.wikipedia.org/wiki/Probability-generating_function

enter image description here

Suppose we want to do this for $n = 2$ then we get after some calculation:

G[p_, z_] =  A[1 - p, z]^2*A[1 - p, A[p, z]/A[1 - p, z]] *(0.5 + 0.5* A[p, A[p, z]/A[1 - p]]/A[1 - p, A[p, z]/A[1 - p]]).

I think that if i would write a programm it becomes like this:

u = z

for i in range n:

if i = n:

  u2 = A[u,n,q] / A[u,n,1-q]

  G(n-i,u,q) = 0.5*(1+ u2)

else:

  u2 = A[u,n,q] / A[u,n,1-q]

  G(n-i,u,q) = A[u,i,1-q]^(2^i-1) * G(i-2,u,q)

  u = u2

However using this algorithm does not transform al substituted u's back to a formula that is only dependent of the variable $q$ and $z$. After some experimention i gained the following expressions which seem to work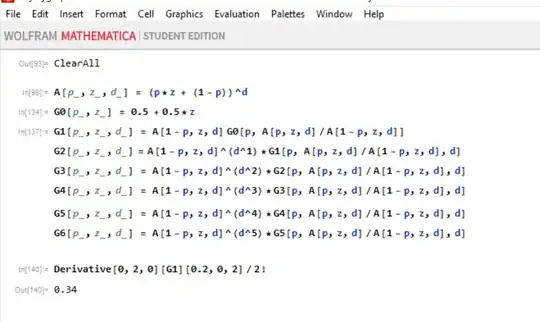enter image description here:

When implementing this i noticed that the code is very slow. Are there any tricks/tips that can make my code faster than it is right now?

Kees Til
  • 123
  • 7
  • 5
    If you don't bother to explain your problem in plain text and type your own equations, why should we bother to type them for you? It's very discouraging to see questions showing little effort. If you expect to inspire anybody to volunteer their time to look at your problem, then start by doing your part. Get the Informed badge by taking and understanding the [tour]. Give context, explain what is the goal, show your efforts to find the solution yourself. You are asking for a favour. – rhermans Jun 28 '18 at 16:27
  • 3
    Here its considered helpful to show your own efforts and share your code in a well formatted form instead of images or links to external files, so we can quickly Copy&Paste your code, test it, and see the problem you are facing. Please help us to help you and [edit] your question accordingly. This question in Meta could be useful. – rhermans Jun 28 '18 at 16:28
  • 1
    Maybe this here helps you to get started, but I agree with rhermans. Someone with more than 600 rep on math.SE should know that good questions require some effort. Please try to improve your question by working on the problem and showing us something that can be copied directly. – halirutan Jun 28 '18 at 17:37
  • 1
    @KeesTil Thanks for taking the [tour] and [edit]ing to show your efforts in well formatted form. I have reverted my downvote. – rhermans Jun 28 '18 at 18:35
  • 1
    i read everything back and it did look lazy indeed i am sorry for that. – Kees Til Jun 28 '18 at 18:39
  • 1
    I can't understand the substitutions part. When and how do you define G for four arguments like in G[n-1,u,p,k] ? – rhermans Jun 28 '18 at 18:44
  • 1
    o true that was an editing mistake, the $k$ is not supposed to be there ill change it right away – Kees Til Jun 28 '18 at 18:55
  • 1
    There are three definitions for G[n,z,p] when does each of these apply? What is the condition that terminates the recursion? (Possibly G[0,z,p] ) I don't know if it's mee been tired or you not making it easy to understand. – rhermans Jun 28 '18 at 22:03
  • the three defitions are the same. The difference between the 2nd and the 3rd is that we substitute $u = \frac{A[z,p]}{A[z.1-p]}$ and apply the same formula but then on $u$ instead of $z$. Thus $G_{n-1} (u,p) = A[u,p] G_{n-2} (\frac{A[u,p]}{A[u.1-p]},p)$ – Kees Til Jun 28 '18 at 22:18
  • Thus by using this substitution each time until we reach $G_0$ is the expression i want in the end which is dependent of the variable $z$, from $n-2$ to $n-3$ we substitute $v = \frac{A[u,p]}{A[u,1-p]}$ etc... – Kees Til Jun 28 '18 at 22:19
  • 1
    Could you rename your variables and functions to match the ones in the image, or at least give an explicit list of the mapping? – Lukas Lang Jun 29 '18 at 07:37
  • 1
    i will do this i will place the mappings under the image – Kees Til Jun 29 '18 at 08:14

1 Answers1

2

The answers to this question address how to make recursive functions of several variables. In a related question, I implicitly suggested computing the body of the function before injecting it into a pure function. For you case, I would do

φ[p_] := (Print["Memoizing ", HoldForm[φ[p]]]; 
  φ[p] = ((1 - p) + p #)^2 &);

G[n_, p_] := (Print["Memoizing ", HoldForm[G[n, p]]];
  With[{x = φ[p][#]^(2^n - 1) G[n - 1, p][φ[p][#]/φ[1 - p][#]]}, 
    G[n, p] = x &]);

G[0, p_] := 1/2 + 1/2 φ[p][#]/φ[p - 1][#] &;

Then, you can use G[n,p][z] to find the expression that depends only on z. For example, 

Simplify[D[G[2, 3][z], z]]
Hector
  • 6,428
  • 15
  • 34