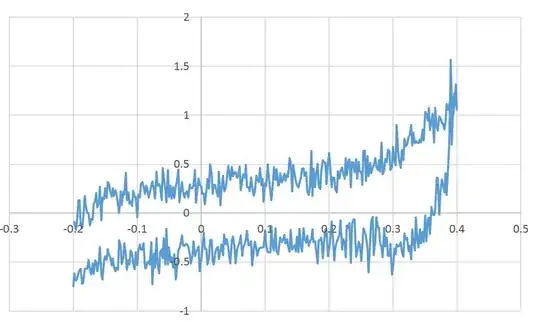
I have this data shown in picture 1 below and I want to filter it. I tried some filters but I couldn't get good results. seems that I didn't choose the best parameters for it.
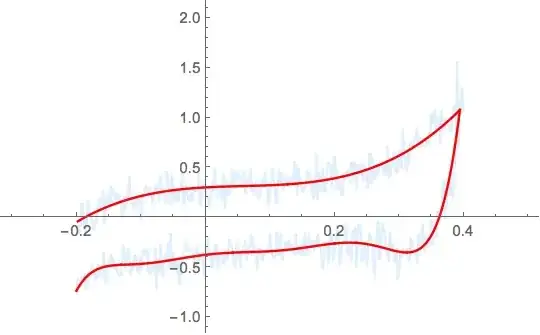
I want to smooth my data (in blue) to be closer to the one in red (without using the data of the red curve.) I appreciate any help.
This is the list I am using in a CSV file (sorry I am a new user in StackExchange and don't know how to upload CSV file here)
data={{-0.198,-0.0934245},{-0.196,-0.17041},{-0.194,-0.0829264},{-0.192,0.134033},{-0.19,0.134033},{-0.188,-0.110921},{-0.186,-0.156413},{-0.184,-0.0479329},{-0.182,0.172526},{-0.18,0.0605469},{-0.178,-0.00244141},{-0.176,0.00105794},{-0.174,-0.128418},{-0.172,-0.058431},{-0.17,-0.068929},{-0.168,0.0955404},{-0.166,0.120036},{-0.164,0.20402},{-0.162,0.0570475},{-0.16,0.0990397},{-0.158,0.270508},{-0.156,-0.0759277},{-0.154,0.158529},{-0.152,0.144531},{-0.15,0.253011},{-0.148,0.15153},{-0.146,0.315999},{-0.144,0.291504},{-0.142,0.214518},{-0.14,0.169027},{-0.138,0.25651},{-0.136,0.176025},{-0.134,0.232015},{-0.132,0.197021},{-0.13,0.081543},{-0.128,0.00105794},{-0.126,0.221517},{-0.124,0.0780436},{-0.122,0.214518},{-0.12,0.190023},{-0.118,0.413981},{-0.116,0.134033},{-0.114,0.211019},{-0.112,0.0955404},{-0.11,0.123535},{-0.108,0.0745443},{-0.106,0.228516},{-0.104,0.162028},{-0.102,0.162028},{-0.1,-0.0409342},{-0.098,0.190023},{-0.096,0.158529},{-0.094,0.295003},{-0.092,0.315999},{-0.09,0.270508},{-0.088,0.197021},{-0.086,0.281006},{-0.084,0.25651},{-0.082,0.158529},{-0.08,0.20752},{-0.078,0.281006},{-0.076,0.322998},{-0.074,0.239014},{-0.072,0.148031},{-0.07,0.424479},{-0.068,0.281006},{-0.066,0.295003},{-0.064,0.270508},{-0.062,0.130534},{-0.06,0.459473},{-0.058,0.36499},{-0.056,0.242513},{-0.054,0.113037},{-0.052,0.438477},{-0.05,0.165527},{-0.048,0.281006},{-0.046,0.148031},{-0.044,0.267008},{-0.042,0.155029},{-0.04,0.274007},{-0.038,0.315999},{-0.036,0.445475},{-0.034,0.109538},{-0.032,0.20752},{-0.03,0.319499},{-0.028,0.218018},{-0.026,0.158529},{-0.024,0.20752},{-0.022,0.221517},{-0.02,0.158529},{-0.018,0.291504},{-0.016,0.25651},{-0.014,0.25651},{-0.012,0.281006},{-0.01,0.441976},{-0.008,0.106038},{-0.006,0.214518},{-0.004,0.354492},{-0.002,0.288005},{1.53*10^-16,0.274007},{0.002,0.197021},{0.004,0.200521},{0.006,0.092041},{0.008,0.232015},{0.01,0.347493},{0.012,0.249512},{0.014,0.497965},{0.016,0.406982},{0.018,0.193522},{0.02,0.291504},{0.022,0.288005},{0.024,0.232015},{0.026,0.169027},{0.028,0.424479},{0.03,0.081543},{0.032,0.249512},{0.034,0.378988},{0.036,0.221517},{0.038,0.253011},{0.04,0.336995},{0.042,0.483968},{0.044,0.424479},{0.046,0.336995},{0.048,0.47347},{0.05,0.375488},{0.052,0.42098},{0.054,0.42098},{0.056,0.357992},{0.058,0.378988},{0.06,0.476969},{0.062,0.235514},{0.064,0.340495},{0.066,0.396484},{0.068,0.357992},{0.07,0.490967},{0.072,0.263509},{0.074,0.263509},{0.076,0.225016},{0.078,0.36499},{0.08,0.267008},{0.082,0.179525},{0.084,0.211019},{0.086,0.382487},{0.088,0.340495},{0.09,0.319499},{0.092,0.459473},{0.094,0.288005},{0.096,0.350993},{0.098,0.116536},{0.1,0.309001},{0.102,0.277507},{0.104,0.497965},{0.106,0.36499},{0.108,0.225016},{0.11,0.134033},{0.112,0.315999},{0.114,0.47347},{0.116,0.336995},{0.118,0.448975},{0.12,0.281006},{0.122,0.298503},{0.124,0.410482},{0.126,0.3125},{0.128,0.336995},{0.13,0.403483},{0.132,0.326497},{0.134,0.399984},{0.136,0.36849},{0.138,0.560954},{0.14,0.522461},{0.142,0.221517},{0.144,0.494466},{0.146,0.385986},{0.148,0.326497},{0.15,0.291504},{0.152,0.26001},{0.154,0.309001},{0.156,0.36499},{0.158,0.455973},{0.16,0.455973},{0.162,0.378988},{0.164,0.41748},{0.166,0.225016},{0.168,0.183024},{0.17,0.26001},{0.172,0.63444},{0.174,0.176025},{0.176,0.455973},{0.178,0.267008},{0.18,0.396484},{0.182,0.504964},{0.184,0.277507},{0.186,0.246012},{0.188,0.427979},{0.19,0.543457},{0.192,0.518962},{0.194,0.511963},{0.196,0.295003},{0.198,0.511963},{0.2,0.613444},{0.202,0.487467},{0.204,0.263509},{0.206,0.36499},{0.208,0.357992},{0.21,0.242513},{0.212,0.211019},{0.214,0.431478},{0.216,0.354492},{0.218,0.431478},{0.22,0.466471},{0.222,0.406982},{0.224,0.350993},{0.226,0.560954},{0.228,0.389486},{0.23,0.52946},{0.232,0.550456},{0.234,0.267008},{0.236,0.518962},{0.238,0.515462},{0.24,0.42098},{0.242,0.550456},{0.244,0.350993},{0.246,0.522461},{0.248,0.424479},{0.25,0.424479},{0.252,0.284505},{0.254,0.63444},{0.256,0.637939},{0.258,0.326497},{0.26,0.585449},{0.262,0.375488},{0.264,0.515462},{0.266,0.406982},{0.268,0.466471},{0.27,0.487467},{0.272,0.560954},{0.274,0.47347},{0.276,0.438477},{0.278,0.543457},{0.28,0.424479},{0.282,0.721924},{0.284,0.396484},{0.286,0.434977},{0.288,0.553955},{0.29,0.518962},{0.292,0.644938},{0.294,0.63444},{0.296,0.438477},{0.298,0.47347},{0.3,0.679932},{0.302,0.522461},{0.304,0.487467},{0.306,0.900391},{0.308,0.616943},{0.31,0.539958},{0.312,0.462972},{0.314,0.648438},{0.316,0.543457},{0.318,0.756917},{0.32,0.683431},{0.322,0.697428},{0.324,0.781413},{0.326,0.79541},{0.328,0.900391},{0.33,0.69043},{0.332,0.819906},{0.334,0.718424},{0.336,0.739421},{0.338,0.714925},{0.34,0.714925},{0.342,0.753418},{0.344,0.721924},{0.346,0.854899},{0.348,0.74292},{0.35,1.03687},{0.352,1.01237},{0.354,0.942383},{0.356,1.07886},{0.358,0.8479},{0.36,0.942383},{0.362,1.01587},{0.364,0.721924},{0.366,1.07886},{0.368,0.882894},{0.37,0.840902},{0.372,0.987874},{0.374,0.970378},{0.376,0.924886},{0.378,0.910889},{0.38,0.8514},{0.382,0.935384},{0.384,1.11385},{0.386,1.05786},{0.388,1.10685},{0.39,1.16634},{0.392,0.700928},{0.394,1.16634},{0.396,1.21883},{0.398,1.12085},{0.4,1.05436},{0.398,1.31681},{0.396,1.12435},{0.394,1.00887},{0.392,1.14884},{0.39,1.56527},{0.388,0.693929},{0.386,0.483968},{0.384,0.186523},{0.382,0.410482},{0.38,0.211019},{0.378,0.295003},{0.376,0.343994},{0.374,0.20752},{0.372,-0.0164388},{0.37,0.357992},{0.368,0.357992},{0.366,0.0255534},{0.364,-0.0199382},{0.362,-0.00594076},{0.36,0.0605469},{0.358,-0.212402},{0.356,-0.0479329},{0.354,-0.058431},{0.352,-0.289388},{0.35,-0.0199382},{0.348,-0.292887},{0.346,-0.191406},{0.344,-0.310384},{0.342,-0.166911},{0.34,-0.348877},{0.338,-0.282389},{0.336,-0.0444336},{0.334,-0.380371},{0.332,-0.289388},{0.33,-0.166911},{0.328,-0.471354},{0.326,-0.33488},{0.324,-0.38737},{0.322,-0.250895},{0.32,-0.271891},{0.318,-0.205404},{0.316,-0.446859},{0.314,-0.390869},{0.312,-0.299886},{0.31,-0.33488},{0.308,-0.341878},{0.306,-0.320882},{0.304,-0.418864},{0.302,-0.362874},{0.3,-0.551839},{0.298,-0.625326},{0.296,-0.313883},{0.294,-0.436361},{0.292,-0.436361},{0.29,-0.247396},{0.288,-0.341878},{0.286,-0.149414},{0.284,-0.453857},{0.282,-0.352376},{0.28,-0.296387},{0.278,-0.149414},{0.276,-0.149414},{0.274,-0.0409342},{0.272,-0.27889},{0.27,-0.429362},{0.268,-0.0374349},{0.266,-0.0829264},{0.264,-0.289388},{0.262,-0.607829},{0.26,-0.359375},{0.258,-0.240397},{0.256,-0.194906},{0.254,-0.156413},{0.252,-0.33138},{0.25,-0.488851},{0.248,-0.320882},{0.246,-0.292887},{0.244,-0.394368},{0.242,-0.446859},{0.24,-0.0619303},{0.238,-0.0654297},{0.236,-0.114421},{0.234,-0.509847},{0.232,-0.103923},{0.23,-0.152913},{0.228,-0.128418},{0.226,-0.450358},{0.224,-0.296387},{0.222,-0.268392},{0.22,-0.369873},{0.218,-0.0724284},{0.216,-0.219401},{0.214,-0.264893},{0.212,-0.285889},{0.21,-0.348877},{0.208,-0.485352},{0.206,-0.219401},{0.204,-0.0864258},{0.202,-0.282389},{0.2,-0.366374},{0.198,-0.443359},{0.196,-0.180908},{0.194,-0.159912},{0.192,-0.310384},{0.19,-0.460856},{0.188,-0.247396},{0.186,-0.27889},{0.184,-0.27889},{0.182,-0.516846},{0.18,-0.366374},{0.178,-0.285889},{0.176,-0.296387},{0.174,-0.166911},{0.172,-0.264893},{0.17,-0.285889},{0.168,-0.33488},{0.166,-0.229899},{0.164,-0.303385},{0.162,-0.268392},{0.16,-0.156413},{0.158,-0.390869},{0.156,-0.341878},{0.154,-0.159912},{0.152,-0.397868},{0.15,-0.236898},{0.148,-0.394368},{0.146,-0.33138},{0.144,-0.348877},{0.142,-0.369873},{0.14,-0.17041},{0.138,-0.394368},{0.136,-0.338379},{0.134,-0.268392},{0.132,-0.306885},{0.13,-0.2229},{0.128,-0.275391},{0.126,-0.299886},{0.124,-0.247396},{0.122,-0.327881},{0.12,-0.418864},{0.118,-0.394368},{0.116,-0.156413},{0.114,-0.380371},{0.112,-0.352376},{0.11,-0.135417},{0.108,-0.397868},{0.106,-0.404867},{0.104,-0.397868},{0.102,-0.33138},{0.1,-0.17391},{0.098,-0.345378},{0.096,-0.348877},{0.094,-0.348877},{0.092,-0.355876},{0.09,-0.366374},{0.088,-0.436361},{0.086,-0.359375},{0.084,-0.292887},{0.082,-0.380371},{0.08,-0.534342},{0.078,-0.285889},{0.076,-0.33138},{0.074,-0.327881},{0.072,-0.180908},{0.07,-0.268392},{0.068,-0.310384},{0.066,-0.352376},{0.064,-0.436361},{0.062,-0.229899},{0.06,-0.292887},{0.058,-0.338379},{0.056,-0.373372},{0.054,-0.513346},{0.052,-0.338379},{0.05,-0.240397},{0.048,-0.275391},{0.046,-0.513346},{0.044,-0.446859},{0.042,-0.338379},{0.04,-0.268392},{0.038,-0.320882},{0.036,-0.219401},{0.034,-0.432861},{0.032,-0.317383},{0.03,-0.376872},{0.028,-0.471354},{0.026,-0.345378},{0.024,-0.366374},{0.022,-0.401367},{0.02,-0.527344},{0.018,-0.485352},{0.016,-0.271891},{0.014,-0.27889},{0.012,-0.453857},{0.01,-0.527344},{0.008,-0.366374},{0.006,-0.366374},{0.004,-0.194906},{0.002,-0.369873},{1.25*10^-16,-0.485352},{-0.002,-0.597331},{-0.004,-0.338379},{-0.006,-0.380371},{-0.008,-0.394368},{-0.01,-0.443359},{-0.012,-0.285889},{-0.014,-0.436361},{-0.016,-0.516846},{-0.018,-0.418864},{-0.02,-0.338379},{-0.022,-0.320882},{-0.024,-0.317383},{-0.026,-0.33488},{-0.028,-0.327881},{-0.03,-0.2264},{-0.032,-0.317383},{-0.034,-0.359375},{-0.036,-0.38387},{-0.038,-0.576335},{-0.04,-0.677816},{-0.042,-0.418864},{-0.044,-0.558838},{-0.046,-0.450358},{-0.048,-0.499349},{-0.05,-0.352376},{-0.052,-0.527344},{-0.054,-0.159912},{-0.056,-0.523844},{-0.058,-0.257894},{-0.06,-0.460856},{-0.062,-0.369873},{-0.064,-0.397868},{-0.066,-0.614827},{-0.068,-0.516846},{-0.07,-0.257894},{-0.072,-0.558838},{-0.074,-0.415365},{-0.076,-0.730306},{-0.078,-0.296387},{-0.08,-0.523844},{-0.082,-0.49585},{-0.084,-0.502848},{-0.086,-0.562337},{-0.088,-0.562337},{-0.09,-0.310384},{-0.092,-0.373372},{-0.094,-0.373372},{-0.096,-0.320882},{-0.098,-0.380371},{-0.1,-0.530843},{-0.102,-0.397868},{-0.104,-0.572835},{-0.106,-0.516846},{-0.108,-0.408366},{-0.11,-0.380371},{-0.112,-0.527344},{-0.114,-0.478353},{-0.116,-0.579834},{-0.118,-0.425863},{-0.12,-0.310384},{-0.122,-0.457357},{-0.124,-0.520345},{-0.126,-0.338379},{-0.128,-0.27889},{-0.13,-0.579834},{-0.132,-0.555339},{-0.134,-0.593831},{-0.136,-0.541341},{-0.138,-0.464355},{-0.14,-0.534342},{-0.142,-0.450358},{-0.144,-0.432861},{-0.146,-0.366374},{-0.148,-0.478353},{-0.15,-0.443359},{-0.152,-0.488851},{-0.154,-0.681315},{-0.156,-0.635824},{-0.158,-0.345378},{-0.16,-0.49585},{-0.162,-0.597331},{-0.164,-0.502848},{-0.166,-0.485352},{-0.168,-0.621826},{-0.17,-0.516846},{-0.172,-0.625326},{-0.174,-0.572835},{-0.176,-0.478353},{-0.178,-0.569336},{-0.18,-0.569336},{-0.182,-0.569336},{-0.184,-0.712809},{-0.186,-0.723307},{-0.188,-0.569336},{-0.19,-0.586833},{-0.192,-0.604329},{-0.194,-0.674316},{-0.196,-0.688314},{-0.198,-0.614827},{-0.2,-0.747803}
};
I used this code and tried to change the parameters but couldn't get the right ones for a smooth curve.
ListLinePlot[{data,
BilateralFilter[data, 2, .14, MaxIterations -> 5]},
PlotStyle -> {Thin, Red}]
I tried to follow this example: Remove noise from data How can we choose the right parameters? Thanks,





TimeSeries. – kirma Jul 10 '18 at 10:55