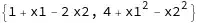Writing System of Equations == 0

Question

I have a system of equations and would like to retrieve the Jacobain w.r.t. to some variables. Now I see that this would be best done if I wrote the equations in a form == 0. Is there an easy way to do the latter? (or simply, retrieve the jacobian of this system of equations?).

Example below:

systemEq = {x1 == 2 x2 - 1,x1^2 == x2^2 - 4}

To make use of the D[] function, I imagine that we would have to rewrite this system as:

systemEqD = {x1 - ( 2 x2 - 1),x1^2 - ( x2^2 - 4)}

where implicitly I am aware that the equations ==0.

Is there an easy way to proceed? (ideally I would like to scale this for a larger number of equations). Many thanks.

The same question has been asked for inequalities, and the answers are basically the same: Is it possible to have Mathematica move all terms to one side of an inequality? — Jens, Jul 16 '18 at 05:20

score 5 · Accepted Answer · answered Jul 15 '18 at 20:24

5

What about this?

Cases[systemEq, Equal[lhs_, rhs_] :> lhs - rhs]

{1 + x1 - 2 x2, 4 + x1^2 - x2^2}

answered Jul 15 '18 at 20:24

Henrik Schumacher

106,770
7
179
309

Perfect, just what I wanted. Many thanks. – user191919 Jul 15 '18 at 20:30
You're welcome. – Henrik Schumacher Jul 15 '18 at 20:30
2

Probably simpler: Equal -> Subtract? (untested) – AccidentalFourierTransform Jul 15 '18 at 22:01

Nasser · Answer 2 · 2018-07-15T21:46:53.850

3

You can also try SubtractSides designed for this sort of thing

ClearAll[x1,x2]
systemEq = {x1==2 x2-1,x1^2==x2^2-4};

First@SubtractSides[#] &/ @systemEq

Mathematica graphics

edited Jul 15 '18 at 21:46

answered Jul 15 '18 at 21:41

Nasser

143,286
11
154
359

score 2 · Answer 3 · answered Jul 15 '18 at 21:50

2

And,

systemEq = {x1 == 2 x2 - 1, x1^2 == x2^2 - 4};

#[[1]] - #[[-1]] == 0 & /@ systemEq

(* {1 + x1 - 2 x2 == 0, 4 + x1^2 - x2^2 == 0} *)

answered Jul 15 '18 at 21:50

Bob Hanlon

157,611
7
77
198

Writing System of Equations == 0

3 Answers3