VectorPlot3D not working as expected (but other functions for same input are)

Question

This is a follow-up question from my previous question. What I was trying to do was to plot the contour plot of the following given scalar function. $$\Phi(x,y,z)=\int_{h=-a}^{a}\int_{k=-b}^{b}\int_{l=-c}^{c}{\dfrac{dh*dy*dl}{\sqrt{(x-h)^2+(y-k)^2+(z-l)^2}}}$$

I used Rubi as an integrating tool to speed up the processing of the code (provided in the accepted answer to the linked question).

After calculating the integral I calculated the Gradient of the scalar function using the Grad[] function provided in Mathematica. Before trying to plot the vector gradient field of the scalar I plotted a contour plot of the same (for some $z$) and then plotted the potential as a function of $x$ and $y$ for some $z=c$; $\Phi(x,y;z=c)$. This code outputted both contour and Plot3D[] function correctly but when I try to plot its vector field using VectorPlot3D[] it gives out a blank plot.

The code would be as follows:

a = 1; b = 1; c = 1;

int0 = Integrate[1/Sqrt[(x - h)^2 + (y - k)^2 + (z - l)^2], l];

int1 = FullSimplify[(int0 /. {l -> c/2}) - (int0 /. {l -> -(c/2)})];

rint2[x_, y_, z_, h_, k_] = Int[int1, k];

rint2def[x_, y_, z_, h_] = rint2[x,y,z,h,b/2] - rint2[x,y,z,h,-(b/2)]// 
Simplify[#, Assumptions -> -(a/2) <= h <= a/2 && -(b/2) <= k <= b/2 && 
   x \[Element] Reals && y \[Element] Reals && z \[Element] Reals] &;

rint3[x_, y_, z_] := NIntegrate[rint2def[x, y, z, h], {h, -(a/2), a/2}]

Now, I plot the ContourPlot for $z=1/4$

ContourPlot[rint3[x, y, 1/4], {x, -2, 2}, {y, -2, 2},ImageSize -> 200]

Which gives the result as

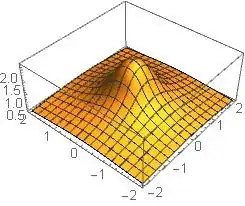
Now, plotting the Plot3D graph for $z=1/4$

Plot3D[rint3[x, y, 1/4], {x, -2, 2}, {y, -2, 2}]

The output of which is

Now when I try to plot the vector field of the scalar potential, the code would be:

VectorPlot3D[Grad[rint3[x, y, z], {x, y, z}], 
{x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

The output is this. :(

I don't get it why is this plot coming up blank. I have plotted other vector fields in a similar way but never got a problem like this by using the Grad[] function. Everything is outputted just as I wanted except for the vector field. What can be done?

Unfortunately your code doesn't evaluate, I cannot reproduce the line ContourPlot — Ulrich Neumann, Jul 16 '18 at 15:09
Use Rubi. Run this notebook after downloading and run my codes in the same notebook. For more info check out the linked questions accepted answer. To download go to -> http://www.apmaths.uwo.ca/~arich/ — diffusiondiver11, Jul 16 '18 at 15:10
My intention was to answer your question, not to do some exercises in rubi! — Ulrich Neumann, Jul 16 '18 at 15:20
No, but the code will not run without Rubi :-/ . It is to improve the performance of code else it takes a large amount of time to calculate with built-in functions. This is why the accepted answer in the linked question recommended this. The Int[] function is specific to Rubi. — diffusiondiver11, Jul 16 '18 at 15:24
Have you tried VectorPlot3D[ Grad[rint3[x, y, z], {x, y, z}]//Evaluate, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}] ? — chris, Jul 16 '18 at 15:48
@chris Thank you so much!!! Exactly what I needed. It worked! :-D — diffusiondiver11, Jul 16 '18 at 15:51

diffusiondiver11 · Accepted Answer · 2018-07-16T16:03:39.223

2

The solution to the problem is as mentioned by @chris in comments of the question

Replace the VectorPlot3D[] command which is

VectorPlot3D[Grad[rint3[x, y, z], {x, y, z}], 
{x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

by

VectorPlot3D[Grad[rint3[x, y, z], {x, y, z}]//Evaluate, 
{x, -2, 2}, {y, -2, 2}, {z, -2, 2}]

"//Evaluate" command has been added.

The output will be

edited Jul 16 '18 at 16:03

answered Jul 16 '18 at 15:58

diffusiondiver11

367
1
9

score 1 · Answer 2 · answered Jul 16 '18 at 15:35

1

If a try a similar problem (without rubi)

VectorPlot3D[Grad[z Exp[-x^2 - y^2], {x, y, z}], {x, -2, 2}, {y, -2, 2},{z,-2,2}]

result is ok. Seems to be a rubi-problem???

answered Jul 16 '18 at 15:35

Ulrich Neumann

53,729
2
23
55

Actually no. It's not a ruby problem I guess because I did the same without ruby and got the same blank output. What you can do is to replace Int[ ] wherever it is used with the built-in function Integrate[ ]. That would do the work without ruby but a bit slower. – diffusiondiver11 Jul 16 '18 at 15:42
The problem is not with Grad or with Rubi. That is why I am confused. Everything else works fine with/without rubi but the problem with vector field remains the same. – diffusiondiver11 Jul 16 '18 at 15:50
Check @chris 's comment above. – diffusiondiver11 Jul 16 '18 at 15:52

VectorPlot3D not working as expected (but other functions for same input are)

2 Answers2