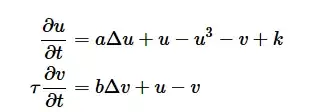I want simulate a reaction-diffusion system described by a PDE called the FitzHugh–Nagumo equation.
The system that has been proposed by Alan Turing as a model of animal coat pattern formation and is exhibited by,
subject to Newman Boundary Conditions and Random Initial Conditions. I'm following the steps in this tutorial https://ipython-books.github.io/124-simulating-a-partial-differential-equation-reaction-diffusion-systems-and-turing-patterns/, but I was not successful. I thought of this code below.
L = 100; (*length of square*)
T = 50; (*Time integration*)
\[Tau] = 0.1; (*parameter*)
a = 0.00028; (*parameter*)
b = 0.005; (*parameter*)
k = -0.005; (*parameter*)
(*system of nonlinear PDE*)
pde = {D[u[t, x, y], t] ==
a*(D[u[t, x, y], x, x] + D[u[t, x, y], y, y]) + u[t, x, y] -
u[t, x, y]^3 - v[t, x, y] + k,
D[v[t, x, y], t] ==
b/\[Tau]*(D[v[t, x, y], x, x] + D[v[t, x, y], y, y]) +
1/\[Tau] u[t, x, y] - 1/\[Tau] v[t, x, y]};
(*Newman boundary condition*)
bc = {(D[u[t, x, y], x] /. x -> -L) ==
0, (D[u[t, x, y], x] /. x -> L) ==
0, (D[u[t, x, y], y] /. y -> -L) ==
0, (D[u[t, x, y], y] /. y -> L) ==
0, (D[v[t, x, y], x] /. x -> -L) ==
0, (D[v[t, x, y], x] /. x -> L) ==
0, (D[v[t, x, y], y] /. y -> -L) ==
0, (D[v[t, x, y], y] /. y -> L) == 0};
(*initial condition*)
ic = {u[0, x, y] == RandomReal[], v[0, x, y] == RandomReal[]};
eqns = Flatten@{pde, bc, ic};
sol = NDSolve[eqns, {u, v}, {t, 0, T}, {x, -L, L}, {y, -L, L}];
Table[DensityPlot[{u[t, x, y]/.sol,v[tx,y]/.sol}, {x, -L, L}, {y, -L, L},
AspectRatio -> Automatic
, PlotRange -> All
, ColorFunction -> "SunsetColors"
, {t, 0, T, 0.1}]
Can someone help me? Thanks in advance.