2

I would like to change the scaling of the x-axis by defining a scaling function. My example is more complicated than the following but I take this one because it is simpler.

What I would like to plot here is the function $x \mapsto x$ in function of $x$ but with a rescaling of the x-axis such that when $x=Log(2)$, the x-axis shows the value 1.

f[x_] := x/Log[2]

Plot[x, {x, 0, 1}, ScalingFunctions -> {f, None}]

However this code doesn't work.

How to make it work ?

StarBucK
  • 2,164
  • 1
  • 10
  • 33

1 Answers1

3

This seems to give the result you want in v10.1:

f[x_] := x/Log[2];

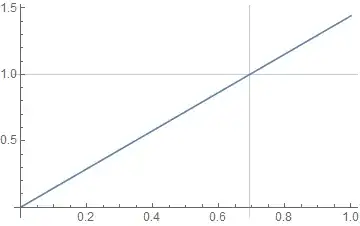
Plot[x, {x, 0, 1}, ScalingFunctions -> {f, InverseFunction[f]}]

Show[%, Ticks -> Automatic, GridLines -> {{Log[2]}, {1}}]

enter image description here

Get Coordinates Tool

If you use the Get Coordinates Tool on the plot above, accessed by right-clicking, you will see that it gives ~= {0.693, 1.00} for the point at which the grid lines cross. I consider this desirable. However if you prefer to have the Get Coordinates Tool return ~= {0.693, 0.693} it would be more direct to skip ScalingFunctions and use a tick generating function directly:

Plot[x, {x, 0, 1}, 
 Ticks -> {Automatic, Charting`ScaledTicks[{InverseFunction[f], f}]}, 
 GridLines -> {{Log[2]}, {Log[2]}}]

It would be possible to make the coordinates of this second plot match those of the first using CoordinatesToolOptions but if that's the desire it's simpler to use Show.

"Elephant in the room"

I interpreted this question as that of making ScalingFunctions work, and answered that, resulting in a somewhat convoluted solution with Show. If that wasn't the actual intent of the question it should be noted that one could scale the function itself directly with essentially the same result:

Plot[f @ x, {x, 0, 1}, GridLines -> {{Log[2]}, {1}}]
Mr.Wizard
  • 271,378
  • 34
  • 587
  • 1,371
  • Thank you. Just to understand, why do I need to put the Ticks->Automatic (indeed without it, the rescaling doesn't show up). But I would like to understand, is it somehow a "refresh" of the x-value to take in account the rescaling ? – StarBucK Jul 24 '18 at 13:07
  • 1
    @StarBucK More or less, yes. Normally scaling doesn't change the labeling but rather the position of the labels. Consider e.g. LogPlot[x, {x, 0, 50}] -- the axis is still labeled 0 to 50. But since you want to change the range of the axis itself you want to force relabeling, as in Show[LogPlot[x, {x, 0, 50}], Ticks -> Automatic] where the axis is now labeled zero to four (approximately). – Mr.Wizard Jul 24 '18 at 13:20