I tried to patch up your code but there were too many bugs and inconsistencies so I just reimplemented it in full. Before you try to implement other big things I'd suggest reading up on Mathematica programming. In particular, if you're going to write procedural code (like one does in python, C, Java, etc.), read about Compile. It will be your friend.
A few issues you had:
- Variables are not sufficiently localized
- Global variables are used inconsistently
- Variable naming is opaque and inconsisten
- Loops are not done functionally, leading to serious performance degredation
Return is used when I should not be
and I think there were actual issues with your Numerov procedure, especially as it related to the Hartree energy
Finally, I found you really do need exchange-correlation to get the expected result. (It took me 3 hours to realize I was using expr^1/3 instead of expr^(1/3) and this converges incredibly slowly and to the wrong number).
With no further ado, here's the code.
First we start with a compiled, general purpose Numerov integrator:
Clear[numerovIntegrator]
numerovIntegrator[vol_, init_] :=
numerovIntegrator[vol, init] =(* caching for later *)
Compile[{
{energy, _Real}, {potential, _Real, 1}
},
Module[
{
psi2 = init[[2]], psi1 = init[[1]], psi0 = 0.,
k2, k1, k0,
c2, c1, c0
},
(* Work backwards from the end;
psi2 is always for the smallest gridpoint *)
Join[
{psi0, psi0},
Table[
(* Numerov step *)
k0 = potential[[i - 2]];
c0 = (1 + vol*k0);
k1 = potential[[i - 1]]; c1 = 2 (1 - 5*vol* k1);
k2 = potential[[i]]; c2 = (1 + vol*k2);
psi2 = (c1*psi1 - c0*psi0)/c2;
psi0 = psi1;
psi1 = psi2,
{i, 3, Length@potential}
]
]
]
];
We use this in the Numerov eigensolver to speed up the bisection significantly (note that most of this code is just protecting the user from kernel crashes):
Clear[numerovEigenSolve]
numerovEigenSolve[
potential_, grid_,
{emin_, emax_}, M_, tol_
] :=
Module[
{
h = grid[[2]] - grid[[1]],
energy, eMin = emin, eMax = emax,
nodes, numiter, psiInit,
psi, norm,
numerov
},
(* Validate potential *)
If[! VectorQ[potential, Internal`RealValuedNumberQ],
Throw@
Failure["InvalidPotential",
<|
"MessageTemplate" :>
"Potential isn't a proper potential vector",
"MessageParameters" -> {}
|>
];
];
If[Length[potential] =!= Length[grid],
Throw@
Failure["InvalidPotential",
<|
"MessageTemplate" :>
"Potential and grid have different lengths (`` and ``)",
"MessageParameters" -> {Length[potential], Length[grid] }
|>
];
];
(* Create integrator potential *)
numerov =
numerovIntegrator[
N[h^2/12](*vol*),
{N[grid[[-1]]*Exp[-grid[[-1]]]],
N[(grid[[-2]])*Exp[-(grid[[-2]])]]} (* initial psi *)
];
(* bisection *)
numiter = \[Infinity];
Do[
energy = N@Mean@{eMin, eMax};
psi =
Reverse@
Check[
numerov[energy, 2*(energy - Reverse@potential)],
Throw@
Failure["InvalidIntegration",
<|
"MessageTemplate" :>
"Numerov integration failed for energy ``",
"MessageParameters" -> {energy}
|>
]
];
nodes = Count[UnitStep[Most[psi]*Rest[psi]], 0];
Which[
nodes == 0 && Abs[psi[[1]]] < tol,
numiter = i;
Break[],
nodes == 0 && psi[[1]] > 0,
eMin = energy,
nodes > 0,
eMax = energy,
True,
Throw@
Failure["InvalidState",
<|
"MessageTemplate" :>
"Solution is negative but nodeless. Numerov integration is \
buggy",
"MessageParameters" -> {}
|>
]
];,
{i, M}
];
(* Straight-up Riemann Integration *)
norm = h*psi.psi;
{energy, psi/Sqrt[norm], numiter}
]
Next we do that Poisson integrator via Verlet:
Clear[verletPoissonSolver]
verletPoissonSolver[grid_] :=
Compile[
{
{f, _Real, 1}
},
Module[
{U0, U1, U2, U, vol},
vol = (grid[[2]] - grid[[1]])^2;
U0 = 0.;
U1 = grid[[2]];
U =
Join[
{U0, U1},
Table[
U2 = 2*U1 - U0 + f[[i - 1]]*vol;
U0 = U1;
U1 = U2,
{i, 3, Length@f}
]
];
U - (U[[-1]] - 1)/grid[[-1]]*grid
]
];
This is again a compiled function that will only be compiled once and will speed up the entire process.
Finally we build our full sloppy DFT implementation. Again, many of the lines here are just protecting the user.
Options[sloppyDFT] =
{
MaxIterations -> 100,
Tolerance -> .001,
"NumerovIterations" -> 50,
"NumerovTolerance" -> 10^-8,
"NumerovSearchRange" -> {-10, 0},
"DampingCoefficient" -> 0.,
"ExchangeCorrelationFunction" ->
Function[{u, r}, -((3./Pi)*(2*u^2)/(r^2*4*Pi))^(1/3)],
"HartreeEnergyFunction" ->
Function[{U, r}, 2*U/r]
};
sloppyDFT[potFunc_, {min_, max_, pts_}, ops : OptionsPattern[]] :=
Catch@
Module[
{
h, grid,
tol =
Replace[
OptionValue[Tolerance],
Except[_?(NumericQ[#] && Positive[#] &)] -> .001
],
maxiter =
Replace[
OptionValue[MaxIterations],
Except[_?(IntegerQ[#] && Positive[#] &)] -> 100
],
energy, energyOld,
u, numerovits,
numSoln,
numERange = OptionValue["NumerovSearchRange"],
numIterMax = OptionValue["NumerovIterations"],
numTol = OptionValue["NumerovTolerance"],
poissonSolver, U,
damp,
hartreeFunc = OptionValue["HartreeEnergyFunction"],
xcFunc = OptionValue["ExchangeCorrelationFunction"],
vNuc, vHartree, vXC,
V,
iterNum = \[Infinity],
hatreeEV, xcEV,
energies
},
h = (max - min)/pts;
grid = min + h*Range[pts] // N;
energy = \[Infinity];
vNuc = potFunc /@ grid;
vHartree = ConstantArray[0, Length@grid];
vXC = ConstantArray[0, Length@grid];
V = vNuc;
poissonSolver = verletPoissonSolver[grid];
energies = ConstantArray[None, maxiter];
damp =
Max@{
Min@{
Replace[OptionValue["DampingCoefficient"],
Except[_?NumericQ] -> 0.], 1.
},
0
};
Do[
energyOld = energy;
If[! VectorQ[vNuc, Internal`RealValuedNumberQ],
Throw@
Failure["InvalidNuclearPotential",
<|
"MessageTemplate" ->
"Nuclear potential is not a real-valued function"
|>
]
];
If[! VectorQ[vHartree, Internal`RealValuedNumberQ],
Throw@
Failure["InvalidHartreePotential",
<|
"MessageTemplate" ->
"Hatree potential is not a real-valued vector"
|>
]
];
If[! VectorQ[vXC, Internal`RealValuedNumberQ],
Throw@
Failure["InvalidHartreePotential",
<|
"MessageTemplate" ->
"Exchange-Correlation potential is not a real-valued vector"
|>
]
];
If[Length@DeleteDuplicates[Length /@ {vNuc, vHartree, vXC}] > 1,
Throw@
Failure["InvalidPotentialDimension",
<|
"MessageTemplate" ->
"Potential components have invalid dimension (``, ``, and \
``)",
"MessageParameters" -> Length /@ {vNuc, vHartree, vXC}
|>
]
];
V = damp*V + (1 - damp)*(vNuc + vHartree + vXC);
numSoln =
numerovEigenSolve[V, grid, numERange, numIterMax, numTol];
If[! ListQ@numSoln && NumericQ@numSoln[[1]],
Throw@
Failure["NumerovFailure",
<|
"MessageTemplate" ->
"Numerov integration failed to find a solution. Returned ``.",
"MessageParameters" -> numSoln
|>
]
];
{energy, u, numerovits} = numSoln;
If[Abs[energy - energyOld] < tol,
iterNum = i;
Break[]
];
U = poissonSolver[-u^2/grid];
vHartree = hartreeFunc[U, grid];
vXC = xcFunc[u, grid];
energies[[i]] = energy;,
{i, maxiter}
];
hatreeEV = h*vHartree.(u^2);
xcEV = .5*h*vXC.(u^2);
<|
"Energy" -> 2*energy - hatreeEV - xcEV,
"Wavefunction" -> Interpolation@Thread[{grid, u}],
"SingleElectronCDF" -> Interpolation@Thread[{grid, U}],
"TotalPotential" -> Interpolation@Thread[{grid, V}],
"Grid" -> grid,
(*"WavefunctionVector"\[Rule]u,
"HatreePotentialVector"\[Rule]U,
"TotalPotentialVector"\[Rule]V,*)
"ComponentPotentials" ->
<|
"NuclearPotential" -> Interpolation@Thread[{grid, vNuc}],
"HartreePotential" -> Interpolation@Thread[{grid, vHartree}],
"ExchangeCorrelationPotential" ->
Interpolation@Thread[{grid, vXC}]
|>,
"ComponentEnergies" ->
<|
"RadialEnergy" -> energy,
"HartreeEnergy" -> hatreeEV,
"ExchangeCorrelationEnergy" -> xcEV
|>,
"IterationCount" -> iterNum,
"IterationEnergies" -> DeleteCases[energies, None]
|>
]
Finally we use it with the parameters in the link and note that we're ~8 times faster now:
dftResult = sloppyDFT[-2/# &, {0, 20, 50000}]; //
AbsoluteTiming // First
11.3862
And we see we have a reasonable wavefunction, the correct energy, and it only took a few iterations:
Plot[dftResult["Wavefunction"][r] // Evaluate, {r, 0, 20},
PlotRange -> All,
PlotLabel ->
TemplateApply["Energy: `Energy` Iterations: `IterationCount`",
dftResult]
]
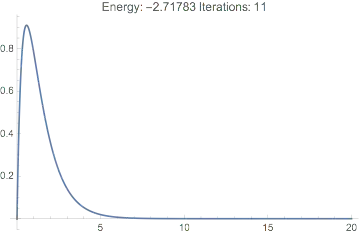
We can also see how the energies converged to this result:
dftResult["IterationEnergies"] // ListLinePlot[#, PlotRange -> All] &

Or look at the pieces of the potential here:
Plot[
Values[dftResult["ComponentPotentials"]][r] // Through // Evaluate,
{r, .1, 20},
PlotRange -> All,
PlotLegends -> Keys[dftResult["ComponentPotentials"]]
]

Update
Just to drive home that the exchange-correlation is needed, we can see what happens if we turn it off. I'll do that by modifying the "ExchangeCorrelationFunction option:
dftResultNoXC =
sloppyDFT[-2/# &, {0, 20, 50000},
"ExchangeCorrelationFunction" -> Function[{u, r}, 0*r]];
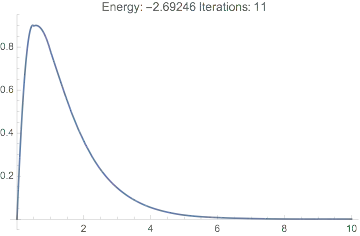
This never converges, the energy is far off, and the wavefunction looks terrible:
Plot[dftResultNoXC["Wavefunction"][r] // Evaluate, {r, 0, 20},
PlotRange -> All,
PlotLabel ->
TemplateApply["Energy: `Energy` Iterations: `IterationCount`",
dftResultNoXC]
]

Further, we can see how the energy changes from iteration to iteration:
dftResultNoXC["IterationEnergies"] // ListLinePlot

And it clearly never converges
We can get convergence by introducing damping:
dftResultNoXC =
sloppyDFT[-2/# &, {0, 20, 50000},
"ExchangeCorrelationFunction" -> Function[{u, r}, 0*r],
"DampingCoefficient" -> .1
];
dftResultNoXC["IterationEnergies"] // ListLinePlot

But the result still isn't quite right:
Plot[dftResultNoXC["Wavefunction"][r] // Evaluate, {r, 0, 20},
PlotRange -> All,
PlotLabel ->
TemplateApply["Energy: `Energy` Iterations: `IterationCount`",
dftResultNoXC]
]

Although interestingly the energy appears not to depend strongly on the damping we choose:
sloppyDFT[-2/# &, {0, 20, 50000},
"ExchangeCorrelationFunction" -> Function[{u, r}, 0*r],
"DampingCoefficient" -> .5
]~Lookup~{"Energy", "IterationCount"}
{-1.94891, 11}








NDSolve. Also tryNDEigensystemfor the Numerov part. It appears to work perfectly. There's also this if J. M. ever comes back and figures out how to do the adaptation he mentions in the comments. – b3m2a1 Jul 31 '18 at 19:39NDEigensystemapproach works too. – b3m2a1 Jul 31 '18 at 21:33poissonisn't initialized before you're trying to index into it. – b3m2a1 Jul 31 '18 at 21:44