Generating stripes on a polygon

Question

I want to create a Graphics3D polygon that has stripes on it. My code is

 Graphics3D[{
   LightBlue, 
   Polygon[{{0, 0, 0}, {0, 2, 0}, {1, 2, 0}, {1, 0, 0}}]}, 
   Boxed -> False,
   Lighting -> {{"Ambient", LightBlue}},
   ViewPoint -> {0.2, 0, 0.2}, 
   RotationAction -> "Clip"]

I want horizontal equidistant stripes on it. Can anyone help?

Answer 1

I commented out some of the options, because they made it difficult for me to see what was exactly happening. [Edit: Change the texture pattern to a variable, to clarify how to modify it. A line pattern given at end.]

stripePattern = 
  Graphics[{Red, Rectangle[{0, 0}, {1, 1/2}], Blue, 
    Rectangle[{0, 1/2}, {1, 1}]}, PlotRangePadding -> 0];

Graphics3D[{Texture[stripePattern], 
  Polygon[{{0, 0, 0}, {0, 2, 0}, {1, 2, 0}, {1, 0, 0}}, 
   VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 4}, {0, 4}}]}, 
 Boxed -> False
 (*,Lighting->{{"Ambient",LightBlue}},ViewPoint->{0.2,0,0.2},RotationAction->"Clip"*)
]

If you have arbitrary polygons, then I don't know how to make the computation of VertexTextureCoordinates easily automatic. (One could compute a projection rather automatically I suppose.) @Mr.Wizard's answer might be easiest in that case.

Graphics3D[{Texture[stripePattern], 
  Polygon[{{0, 0, 0}, {0, 0, 2}, {0, 2, 2}, {0, 3, 1}, {0, 2, 0}}, 
   VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1, 4}, {1/2, 6}, {0, 4}}]}, 
 Boxed -> False
]

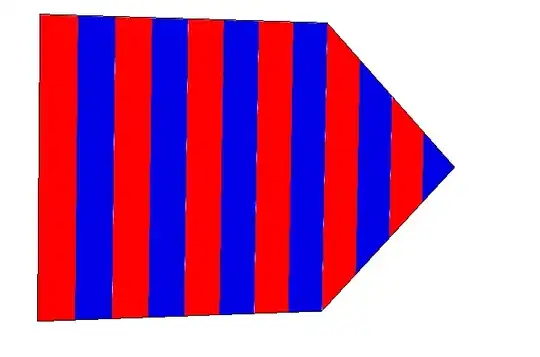
Addendum - Edited

Here's a projection function that projects the polygon onto the texture coordinate system. (Please excuse not putting in full error checking.)

I have edited the code to replace the pattern by lines instead of stripes, per the OP's query.

project[polygonVertices_, stripeDirection_, nStripeMultiplier_] := 
  Module[{normal, e1, e2},
    normal = 
     Normalize@
      Catch[(If[Chop[#] != {0, 0, 0}, Throw[#]] &@(Cross @@ Differences[#])) & /@ 
         Partition[polygonVertices, 3, 1, 1];];
    e2 = normal\[Cross]Normalize[stripeDirection];
    e1 = e2\[Cross]normal;
    polygonVertices.Transpose[{e1, nStripeMultiplier e2}]
    ] /; Length[polygonVertices] >= 3;

linePattern = 
  Graphics[{Thickness[0.15], Red, Line[{{0, 1/2}, {1, 1/2}}]}, 
   PlotRangePadding -> 0, PlotRange -> {{0, 1}, {0, 1}}];

With[{poly = 
   Table[RandomReal[{1, 2}] {Cos[t], Sin[t], 
      Cos[t] - 2 Sin[t]}, {t, π/6, 2 π, π/6}]}, 
 Graphics3D[{Texture[linePattern], 
   Polygon[poly, 
    VertexTextureCoordinates -> project[poly, {-2, -2, 2}, 4]]}, 
  Lighting -> {{"Ambient", White}}]
 ]

Answer 2

Perhaps you can parametrize your polygon and use ParametricPlot3D which takes MeshFunctions / MeshShading options. Alternately you could try interpolating your data and using ListSurfacePlot3D which also takes these options.

An example from the MeshFunctions documentation (using Plot3D):

Plot3D[
 (x^2 - y^2)/(x^2 + y^2)^2, {x, -1.5, 1.5}, {y, -1.5, 1.5},
 BoxRatios -> Automatic, 
 PlotPoints -> 25,
 MeshFunctions -> {#3 &},
 MeshStyle -> Purple, 
 MeshShading -> {None, Green, None, Yellow}
]

Another from the ParametricPlot3D documentation:

ParametricPlot3D[
  {(2 + Cos[v]) Cos[u], (2 + Cos[v]) Sin[u], Sin[v]},
  {u, 0, 2 Pi}, {v, 0, 2 Pi},
  Mesh -> 15,
  MeshShading -> {Red, Blue},
  MeshFunctions -> {#4 &}
]

And finally one for ListSurfacePlot3D

ListSurfacePlot3D[data, MaxPlotPoints -> 50, Mesh -> 30, Axes -> None, 
 MeshFunctions -> (#1 - #2 + #3 &), MeshShading -> {None, Yellow}]

Answer 3

Using improved Texture capability in v14:

p1 = Graphics[{AbsoluteThickness[18], 
   Table[{If[EvenQ[Floor@(10 k/2)], Red, Blue], 
     Line[{{k, -1}, {k + 1, 1}}]}, {k, -2, 2, .2}]}, PlotRange -> 1];
Graphics3D[{Texture[p1], Polygon[{{0, 0, 0}, {0, 2, 0}, {1, 2, 0}, {1, 0, 0}}]}]

Using @MichaelE2's example:

With[{poly = 
   Table[RandomReal[{1, 2}] {Cos[t], Sin[t], 
      Cos[t] - 2 Sin[t]}, {t, \[Pi]/6, 2 \[Pi], \[Pi]/6}]}, 
 Graphics3D[{Texture[p1], 
   Polygon[poly]}, 
  Lighting -> {{"Ambient", White}}]
 ]