Nonlinear system of ODEs with boundary conditions

Question

I'm trying solve this problem:

g'(r) = a(r)g(r)/r, (1/r)a'(r) = g(r)^2-1

which have the following boundary conditions: a(0)=n and g(infinity)=1, where n>=1.

I have problem with the error for n=1[hence, failed for the other n values as well.]:

"Infinite expression 1/0.^2 encountered"

using DSolve directly.

A work colleague solved for the values n=1,2,5,10 using the software MAPLE. But, I don't know to use MAPLE and I would like to get these results by Mathematica. Below are the plots found by MAPLE.

Please include the Mathematica code text in your question. — xzczd, Aug 08 '18 at 16:58
Welcome to Mma.SE. Start by taking the [tour] now and learning about asking and what's on-topic. Always [edit] if improvable, show due diligence, give brief context, include minimal working example of code and data you are working on in formatted form. By doing all this you help us to help you and likely you will inspire great answers. The site depends on participation, as you receive give back: vote and answer questions, keep the site useful, be kind, correct mistakes and share what you have learned — rhermans, Aug 08 '18 at 17:10
See this previous answer. Compactifying in MMA is rather trivial. — Hector, Aug 08 '18 at 17:10
I find that DSolve does not produce an error message but instead returns unevaluated, meaning that it cannot solve the problem.. — bbgodfrey, Aug 08 '18 at 21:34
Maple code:sol := proc (n) options operator, arrow; dsolve([(D(g))(r) = a(r)*g(r)/r, (D(a))(r)/r = g(r)^2-1, a(1/100000) = n, g(10) = 1], numeric) end proc;plots:-display(seq({plots:-odeplot(sol(n), [r, g(r)], linestyle = n, color = ColorTools:-Color([1/n, 1/(1+n), 1/(n+4)]))}, n = 1 .. 7));plots:-display(seq({plots:-odeplot(sol(n), [r, a(r)], linestyle = n, color = ColorTools:-Color([1/n, 1/(1+n), 1/(n+4)]))}, n = 1 .. 7)); — Mariusz Iwaniuk, Aug 11 '18 at 17:17

bbgodfrey · Answer 1 · 2018-08-11T18:15:38.280

Error in boundary condition corrected

To solve this ODE system, begin by determining its behavior near r == 0.

Series[{g'[r] - (a[r] g[r])/r, a'[r]/r + 1 - g[r]^2}, {r, 0, 2}] // Normal;
Thread[Flatten@CoefficientList[r % /. a[0] -> n, r] == 0];
Solve[%, {a'[0], a''[0], a'''[0], a''''[0], g[0], g'[0], g''[0], g'''[0]}]

(* a'[0] -> 0, a''[0] -> -1, a'''[0] -> 0, a''''[0] -> 0,
   g[0] -> 0, g'[0] -> 0, g''[0] -> 0, g'''[0] -> 0  *)

In other words, g[r] vanishes to all orders at the origin for most values of n. However, if n is a positive integer, the same set of commands leaves Derivative[n][g][0] undetermined. So, g[eps] is approximately proportional to eps^n. Next, solve the equations numerically by shooting, using the method previously employed here and elsewhere on this site. (As noted in my comment above, DSolve returns unevaluated when applied to these equations.) A typical calculation for n == 5 is given by

eps = 10^-5; end = 20;
sp = ParametricNDSolveValue[{g'[r] == a[r] g[r]/r, a'[r]/r == g[r]^2 - 1, 
    a[eps] == n0, g[eps] == eps^n0 gp, 
    WhenEvent[g[r] > 101/100, {bool = 1, "StopIntegration"}], 
    WhenEvent[a[r] < 0, {bool = 0, "StopIntegration"}]}, 
    {a[r], g[r]}, {r, eps, end + 5}, {gp, wp0, n0}, 
    WorkingPrecision -> wp0, Method -> "StiffnessSwitching"];
bl = 0; bu = 2; imax = 100; wp = 75; n = 5;
Do[bool = -1; bmiddle = (bl + bu)/2; st = sp[bmiddle, wp, n]; 
    rm = (First[st] /. r -> "Domain")[[1, 2]]; 
    If[bool == 0, bl = bmiddle, bu = bmiddle]; ip = i; 
    If[bool == -1, Return[]], {i, imax}]; 
s[n] = st;

For larger values of n, wp must be increased. For instance, with n = 10, wp = 90 is required. Results for n = {1, 2, 5, 10} are plotted below.

Plot[{s[1], s[2], s[5], s[10]}, {r, eps, 10}, PlotRange -> All, AxesLabel -> {r, "a, g"}, 
    ImageSize -> Large, LabelStyle -> {Black, Bold, Medium}]

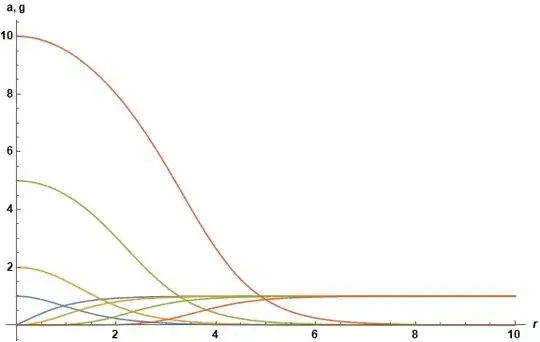
The solutions takes no more than several seconds each.

I have appreciated your answer. Thank you very much @bbgodfrey. You've already been very helpful. A friend got solve also for values n>1, but he used the software MAPLE. I don't know to use the MAPLE, but I'll try to use your answer like a procedure. — Andrey, Aug 10 '18 at 01:49
@AndréCavalcante Because the ODEs are nonlinear, not all boundary conditions are consistent with them. In this case, I believe that A[0] == 1 is the only consistent boundary condition, unless you are willing to accept g[r] == 0 as a solution. Perhaps, I could get Mathematica to produce numerical solutions for other values of n, but they would be incorrect, I believe. — bbgodfrey, Aug 10 '18 at 01:58
I have edited my question and added the plots obtained by MAPLE. Indeed, using its answer it was not possible to solve for values greater than n == 1. In addition, by behavior near r == 0, I have noticed that for n == 2, for example, leaves g''[0] undetermined. — Andrey, Aug 11 '18 at 16:58
@AndréCavalcante I just realized that I had made an error in the g[eps] boundary condition. In fact, any positive integer value of n gives a valid solution. Sorry. — bbgodfrey, Aug 11 '18 at 18:17

Mariusz Iwaniuk · Accepted Answer · 2018-08-12T09:40:17.183

4

Another way:

eps = 10^-10; end = 10;
sol[n_] := NDSolve[
{g'[r] == a[r]*g[r]/r, a'[r]/r == g[r]^2 - 1, a[eps] == n, g[end] == 1}
,{a[r], g[r]}, {r, eps, end}, Method -> {"Shooting", 
"StartingInitialConditions" -> {a[end] == eps, g[end] == (1 - eps)}}];

Plot[Evaluate[g[r] /. sol[#] & /@ {1, 2, 5, 10}], {r, eps, end},PlotRange -> All, 
PlotLegends -> {"n=1", "n=2", "n=5", "n=10"}, PlotLabels -> "g(r)"]
Plot[Evaluate[a[r] /. sol[#] & /@ {1, 2, 5, 10}], {r, eps, end}, PlotRange -> All, 
PlotLegends -> {"n=1", "n=2", "n=5", "n=10"}, PlotLabels -> "a(r)"]

For larger values e.g.end=20:

eps = 10^-20; end = 20;
sol[n_] := NDSolve["Code the same",WorkingPrecision -> 25];
Plot["Code the same"] // Quiet(*Error messages form InterpolatingFunction to Quiet *)

edited Aug 12 '18 at 09:40

answered Aug 12 '18 at 09:17

Mariusz Iwaniuk

13,841
1
25
41

Thanks for your answer, you've been a big help. – Andrey Aug 12 '18 at 18:49
Dear @MariuszIwaniuk, I was very grateful for the help on this occasion. Now, if it is possible to help again, how could I make a projection of these solutions in the plan? That is, would it be possible to make a density plot? – Andrey Jul 19 '19 at 19:19

Nonlinear system of ODEs with boundary conditions

2 Answers2

Linked